题目内容
10.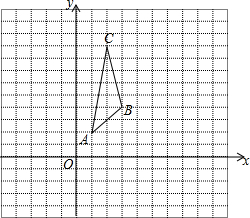 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).(1)画出△ABC关于y轴对称的△A1B1C1.
(2)画出△A1B1C1向右平移8个单位后得到的△A2B2C2.
(3)直接写出△ABC上点M(x,y)在上述变换过程中得到△A2B2C2上的对应点M2的坐标.
分析 (1)首先确定A、B、C三点关于y轴对称的点的位置,再连接即可;
(2)首先确定A1、B1、C1三点向右平移8个单位后的对应点位置,再连接即可;
(3)根据点的坐标的变化规律:向右平移几个单位,横坐标加几可得M2的坐标.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
(3)对应点M2的坐标(-x+8,y).
点评 此题主要考查了轴对称变换和平移变换,关键是掌握图形是由点组成的,作轴对称变换和平移变换就是找出图形的关键点的对称点和对应点的位置.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
18.已知x,y满足$\left\{\begin{array}{l}{2x-3y=1①}\\{3x-2y=5②}\end{array}\right.$,如果①×a+②×b可整体得到x+11y的值,那么a,b的值可以是( )
| A. | a=2,b=-1 | B. | a=-4,b=3 | C. | a=1,b=-7 | D. | a=-7,b=5 |
5.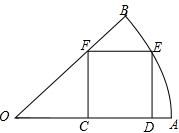 如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )
如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )
 如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )
如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )| A. | π:8 | B. | 5π:8 | C. | $\sqrt{3}$π:4 | D. | $\sqrt{5}$π:4 |
2.下列运算正确的是( )
| A. | a2•a2=a4 | B. | (a-b)2=a2-b2 | C. | 2+$\sqrt{2}$=2$\sqrt{2}$ | D. | (-a3)2=-a6 |
 已知:⊙O的半径为5,PO=3
已知:⊙O的半径为5,PO=3 如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F. 如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.
如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.