题目内容
5．
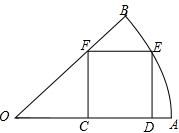如图，在圆心角为45°的扇形内有一正方形CDEF，其中点C、D在半径OA上，点F在半径OB上，点E在$\widehat{AB}$上，则扇形与正方形的面积比是（ ）| A． | π：8 | B． | 5π：8 | C． | $\sqrt{3}$π：4 | D． | $\sqrt{5}$π：4 |
分析 连接OE，设正方形的边长为a．根据等腰直角三角形的性质，得OC=CF=a，在直角三角形OFC中，根据勾股定理列方程，用a表示出r的值，再根据扇形及正方形的面积公式求解．
解答 
解：连接OE，设正方形的边长为a，则正方形CDEF的面积是a2，
在Rt△OCF中，a2+（2a）2=r2，即r=$\sqrt{5}$a，
扇形与正方形的面积比=$\frac{45π{r}^{2}}{360}$：a2=$\frac{45π{（\sqrt{5}a）}^{2}}{360}$：a2=5π：8．
故选B．
点评 本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键．
练习册系列答案
相关题目
15．一艘轮船只有在涨潮的时候才能驶入港口，已知该港口每天涨潮的时间为早：5：00至7：00和下午5：00至6：00，则该船在一昼夜内可以进港的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{20}$ | D． | $\frac{1}{12}$ |
16．
已知二次函数y=ax2+bx=c（a≠0）的图象如图所示，与y轴相交一点C，与x轴负半轴相交一点A，且OA=OC，有下列5个结论：
①abc＞0；②b＜a+c；③4a+2b+c＞0；④2a+b=0；⑤c+$\frac{1}{a}$=-2．
其中正确的结论有 （ ）
已知二次函数y=ax2+bx=c（a≠0）的图象如图所示，与y轴相交一点C，与x轴负半轴相交一点A，且OA=OC，有下列5个结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④2a+b=0；⑤c+$\frac{1}{a}$=-2．
其中正确的结论有 （ ）
| A． | ③④⑤ | B． | ③④ | C． | ①②③ | D． | ②③④ |
13．方程3x2-2$\sqrt{6}$x+2=0的根的情况是（ ）
| A． | 无实根 | B． | 有两个等根 | C． | 有两个不等根 | D． | 有分数根 |
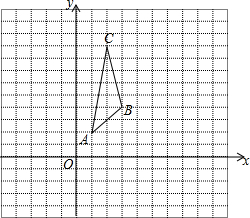在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（1，2），B（3，4），C（2，9）．
14．
直线l1∥l2，一块含45°角的直角三角板，如图放置，∠1=42°，则∠2等于（ ）
直线l1∥l2，一块含45°角的直角三角板，如图放置，∠1=42°，则∠2等于（ ）| A． | 97° | B． | 93° | C． | 87° | D． | 83° |