题目内容
7.计算与化简:(1)$\sqrt{8}$-2sin45°-|1-$\sqrt{2}$|
(2)$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$•(x-$\frac{1}{x}$)
分析 (1)原式第一项化为最简二次根式,第二项利用特殊角的三角函数值计算,第三项利用绝对值的代数意义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,约分即可得到结果.
解答 解:(1)原式=2$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$-$\sqrt{2}$+1=1;
(2)原式=$\frac{x(x-1)}{(x-1)^{2}}$•$\frac{(x+1)(x-1)}{x}$=x+1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17.下图中不能表示y是x的函数是( )
| A. |  | B. |  | C. |  | D. |  |
18.已知,圆锥的高h=$2\sqrt{3}$cm,底面半径r=2cm,则圆锥的侧面积为( )cm2.
| A. | 4$\sqrt{3}$π | B. | 8π | C. | 12π | D. | (4$\sqrt{3}$+4)π |
2. 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
19.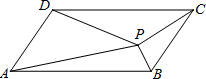 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )| A. | S1+S2=S3+S4 | B. | S1+S2>S3+S4 | C. | S1+S3=S2+S4 | D. | S1+S2<S3+S4 |
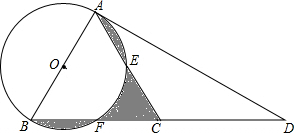 如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F
如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F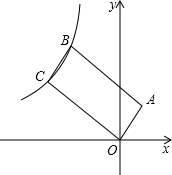 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.