题目内容
15.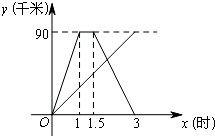 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.根据图象完成下列问题:
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.根据图象完成下列问题:(1)甲前往B地时的平均速度为90,返回A地时的平均速度为60;
(2)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?
分析 (1)根据速度等于路程除以时间进行解答即可;
(2)首先设y与x之间的函数关系式为y=kx+b,根据图象可得直线经过(1.5,90)(3,0),利用待定系数法把此两点坐标代入y=kx+b,即可求出一次函数关系式;
(3)利用甲从B地返回A地的过程中,y与x之间的函数关系式算出y的值,即可得到2小时时骑摩托车所行驶的路程,再根据路程与时间算出摩托车的速度,再用总路程90千米÷摩托车的速度可得乙从A地到B地用了多长时间.
解答 解:(1)甲前往B地时的平均速度为$\frac{90}{1}=90$千米/小时,返回A地时的平均速度为$\frac{90}{3-1.5}=60$千米/小时,
故答案为:90;60;
(2)设甲从B地返回A地的过程中,y与x之间的函数关系式为y=kx+b(k≠0),根据题意得:
$\left\{\begin{array}{l}{3k+b=0}\\{1.5k+b=90}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-60}\\{b=180}\end{array}\right.$.
故y=-60x+180(1.5≤x≤3);
(3)当x=2时,y=-60×2+180=60,
∴骑摩托车的速度为60÷2=30(千米/时),
∴乙从A地到B地用时为90÷30=3(小时).
点评 此题主要考查了一次函数的应用,关键是看懂图象所表示的意义,利用待定系数法求出甲从B地返回A地的过程中,y与x之间的函数关系式.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
3.平行四边形、矩形、菱形、正方形都具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对角线相等 | D. | 轴对称图形 |
20.下列说法正确的是( )
| A. | 平方得9的数只有一个 | B. | 立方得-8的数只有一个 | ||
| C. | 平方得-9的数只有一个 | D. | 立方得9的整数只有一个 |
5. 如图,⊙O的弦AB=18,M是AB的中点,且OM=12,则⊙O的半径等于( )
如图,⊙O的弦AB=18,M是AB的中点,且OM=12,则⊙O的半径等于( )
 如图,⊙O的弦AB=18,M是AB的中点,且OM=12,则⊙O的半径等于( )
如图,⊙O的弦AB=18,M是AB的中点,且OM=12,则⊙O的半径等于( )| A. | 8 | B. | 2 | C. | 10 | D. | 15 |
 如图,在四边形ABCD中,线段BD垂直平分AC,且相交于点0,∠1=∠2,求证:四边形ABCD是菱形.
如图,在四边形ABCD中,线段BD垂直平分AC,且相交于点0,∠1=∠2,求证:四边形ABCD是菱形.