题目内容
14.已知$\frac{4x+5}{3}$不大于2x,那么x的取值范围是x≥$\frac{5}{2}$.分析 根据题意列出不等式,依据解一元一次不等式基本步骤:去分母、移项、合并同类项、系数化为1可得.
解答 解:根据题意得$\frac{4x+5}{3}$≤2x,
去分母,得:4x+5≤6x,
移项,得:4x-6x≤-5,
合并同类项,得:-2x≤-5,
系数为化为1,得:x≥$\frac{5}{2}$,
故答案为:x≥$\frac{5}{2}$.
点评 本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
6. 如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.
如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.
 如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.
如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段8cm,若AP=$\frac{1}{2}$PB,则这条绳子的原长为( )cm.| A. | 12 | B. | 24 | C. | 20 或24 | D. | 12或24 |
4. △ABC中,∠C=90°,D是AC边上一点,且CD=CB,AD=BD,则tanA的值是( )
△ABC中,∠C=90°,D是AC边上一点,且CD=CB,AD=BD,则tanA的值是( )
 △ABC中,∠C=90°,D是AC边上一点,且CD=CB,AD=BD,则tanA的值是( )
△ABC中,∠C=90°,D是AC边上一点,且CD=CB,AD=BD,则tanA的值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}}{2}$ | D. | 不能确定 |
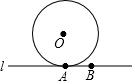 如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.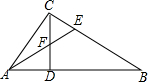 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.