题目内容
19.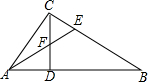 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.(1)求△ABC的面积及高CD;
(2)△ABC的角平分线AE交CD于点F,求证:∠CFE=∠CEF.
分析 (1)根据三角形的面积公式列式计算即可;
(2)根据直角三角形的性质和角平分线的定义证明即可.
解答 解:(1)由题意得,△ABC的面积=$\frac{1}{2}$×AB×CD=$\frac{1}{2}×6×8=24$,
$\frac{1}{2}$×AB×CD=$\frac{1}{2}$×AC×BC,
即$\frac{1}{2}$CD×10=$\frac{1}{2}$6×8,
解得CD=$\frac{24}{5}$;
(2)∵∠ACB=90°,
∴∠CAE+∠CEF=90°,
∵CD是AB边上的高,
∴∠FAD+∠AFD=90°,
∵AE是∠CAB的平分线,
∴∠CAE=∠FAD,
∴∠CEF=∠AFD,
又∵∠AFD=∠CFE,
∴∠CFE=∠CEF.
点评 本题考查的是勾股定理的应用、直角三角形的性质,掌握直角三角形的面积公式、直角三角形的两锐角互余是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
16.某课外小组的同学们实践活动中调查了20户家庭某月用电量,如表所示:
则这户家庭用电量的众数和中位数分别是( )
| 用电量(度) | 120 | 140 | 160 | 180 | 220 |
| 户数 | 2 | 4 | 5 | 7 | 2 |
| A. | 180,160 | B. | 160,180 | C. | 160,160 | D. | 180,180 |
4.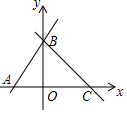 如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )
 如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )| A. | (3$\sqrt{2}$,0) | B. | (6,0) | C. | (3$\sqrt{3}$,0) | D. | (5,0) |