题目内容
 如图,在△ABC中,∠B=45°,∠C=30°,D是AC中点,DE⊥BC,求
如图,在△ABC中,∠B=45°,∠C=30°,D是AC中点,DE⊥BC,求| BE |
| EC |
考点:三角形中位线定理,等腰直角三角形
专题:
分析:如图,过点A作AF⊥BC于点F,易证DE是△AFC的中位线,利用三角形中位线的定义得到EC=EF,DE=
AF.通过解直角三角形得到CE的长度;然后由等腰直角三角形的性质得到BF=AF.则易求
的值.
| 1 |
| 2 |
| BE |
| EC |
解答: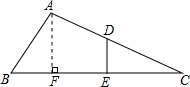 解:如图,过点A作AF⊥BC于点F.
解:如图,过点A作AF⊥BC于点F.
∵DE⊥BC,
∴AF∥DE.
又∵D是AC中点,
∴DE是△AFC的中位线,
∴点E是FC的中点即EC=EF,DE=
AF.
又∵∠C=30°,∠B=45°,
∴EC=ED•cot30°=
ED=
AF,BF=AF,
∴BE=BF+CE=AF+
AF,
∴
=
=
.
 解:如图,过点A作AF⊥BC于点F.
解:如图,过点A作AF⊥BC于点F.∵DE⊥BC,
∴AF∥DE.
又∵D是AC中点,
∴DE是△AFC的中位线,
∴点E是FC的中点即EC=EF,DE=
| 1 |
| 2 |
又∵∠C=30°,∠B=45°,
∴EC=ED•cot30°=
| 3 |
| ||
| 2 |
∴BE=BF+CE=AF+
| ||
| 2 |
∴
| BE |
| EC |
AF+
| ||||
|
2
| ||
| 3 |
点评:本题考查了三角形中位线定理和等腰直角三角形.此题将EC、BE的长度转化为AF的长度,通过约分求得
的值.
| BE |
| EC |

练习册系列答案
相关题目
如果方程5x+5y-2+3kx-2ky-5k=0(k为常数)是关于x的一元一次方程,那么k的值应该是( )
| A、0 | ||
B、
| ||
C、-
| ||
D、
|
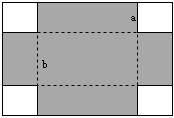 如图,有一张长方形纸板,在它的四角各切去一个同样的正方形,然后将四周突出补分折起,制成一个高为a的长方体形状的无盖纸盒,如果纸盒的容积为4a2b,底面长方形的一边长为b(b<4a),求长方形纸板的长和宽.
如图,有一张长方形纸板,在它的四角各切去一个同样的正方形,然后将四周突出补分折起,制成一个高为a的长方体形状的无盖纸盒,如果纸盒的容积为4a2b,底面长方形的一边长为b(b<4a),求长方形纸板的长和宽.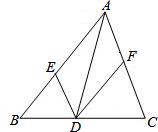 已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F.
已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F.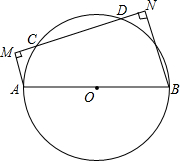 AB为⊙O的直径,CD为弦,AM⊥CD于M,BN⊥CD于N.
AB为⊙O的直径,CD为弦,AM⊥CD于M,BN⊥CD于N. 如图,已知线段AB,请用尺规按下列要求作图:
如图,已知线段AB,请用尺规按下列要求作图: