题目内容
7.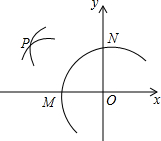 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )| A. | M-n=-3 | B. | m+n=-3 | C. | m-n=3 | D. | m+n=3 |
分析 根据作图过程可得P在第二象限角平分线上,由角平分线的性质:角的平分线上的点到角的两边的距离相等可得|m|=|n-3|,再根据P点所在象限可得横纵坐标的和为0,进而得到m与n的数量关系.
解答 解:根据作图方法可得点P在第二象限角平分线上,
则P点横纵坐标的和为0,
故m+n-3=0,
整理得:m+n=3,
故选:D.
点评 此题主要考查了每个象限内点的坐标特点,以及角平分线的性质,关键是掌握各象限角平分线上的点的坐标特点|横坐标|=|纵坐标|.

练习册系列答案
相关题目
17.等腰三角形的一个角为50°,则它的底角为( )
| A. | 50° | B. | 65° | C. | 50°或65° | D. | 80° |
15.先化简,再求值:($\frac{2x+1}{{{x^2}-4x+4}}$-$\frac{1}{x-2}$)÷$\frac{x+3}{{{x^2}-4}}$,其中x是不等式3x+7>1的负整数解.
2.下列多项式能进行因式分解的是( )
| A. | x2-y | B. | x2+1 | C. | x2-6x | D. | x2+y+y2 |
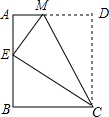 如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.
如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.