题目内容
15.先化简,再求值:($\frac{2x+1}{{{x^2}-4x+4}}$-$\frac{1}{x-2}$)÷$\frac{x+3}{{{x^2}-4}}$,其中x是不等式3x+7>1的负整数解.分析 先根据分式混合运算的法则把原式进行化简,求出x的值代入进行计算即可.
解答 解:原式=[$\frac{2x+1}{{(x-2)}^{2}}$-$\frac{1}{x-2}$]÷$\frac{x+3}{(x+2)(x-2)}$
=$\frac{x+3}{{(x-2)}^{2}}$•$\frac{(x+2)(x-2)}{x+3}$
=$\frac{x+2}{x-2}$.
解不等式3x+7>1,得x>-2,
∵x是不等式的负整数解,
∴x=-1.
当x=-1时,原式=$\frac{-1+2}{-1-2}$=-$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3. 如图,CO⊥AB,垂足为点O,若∠1=∠2,则∠DOE等于( )
如图,CO⊥AB,垂足为点O,若∠1=∠2,则∠DOE等于( )
 如图,CO⊥AB,垂足为点O,若∠1=∠2,则∠DOE等于( )
如图,CO⊥AB,垂足为点O,若∠1=∠2,则∠DOE等于( )| A. | 60° | B. | 80° | C. | 90° | D. | 100° |
10.若点P(a,a-3)在第四象限,则a的取值范围是( )
| A. | a<0 | B. | a>3 | C. | -3<a<0 | D. | 0<a<3 |
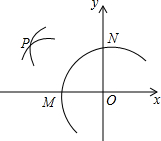 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )