题目内容
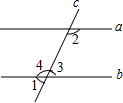如图，先填空后证明．已知：∠1+∠2=180°，求证：a∥b．
证明：∵∠1=∠3
∠1+∠2=180°
∴∠3+∠2=180°
∴a∥b
请你再写出另一种证明方法．
考点：平行线的判定
专题：推理填空题
分析：由条件结合对顶角相等可求得∠2+∠3=180°，可证明a∥b，据此填空即可；也可利用∠1=∠4来证明．
解答：
证明：∵∠1=∠3 对顶角相等，
∠1+∠2=180° 已知，
∴∠3+∠2=180° 等量代换，
∴a∥b 同旁内角互补，两直线平行．
故答案为：对顶角相等；已知；等量代换；同旁内角互补，两直线平行．
另一种证法：
∵∠1+∠2=180°，∠1+∠4=180°，
∴∠2=∠4，
∴a∥b．
∠1+∠2=180° 已知，
∴∠3+∠2=180° 等量代换，
∴a∥b 同旁内角互补，两直线平行．
故答案为：对顶角相等；已知；等量代换；同旁内角互补，两直线平行．
另一种证法：
∵∠1+∠2=180°，∠1+∠4=180°，
∴∠2=∠4，
∴a∥b．
点评：本题主要考查平行线的判定，掌握平行线的性质和判定是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补，④a∥b，b∥c?a∥c．
练习册系列答案
名校课堂系列答案
相关题目
如图，不能推出a∥b的条件是（ ）| A、∠1=∠3 |
| B、∠1=∠4 |
| C、∠2=∠4 |
| D、∠2+∠3=180° |
如图所示，如果∠1=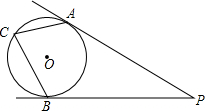
如图，PA、PB是⊙O的两条切线，切点分别是A、B，点C在⊙O上，若∠P=30°，则∠ACB=