题目内容
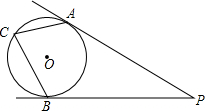 如图,PA、PB是⊙O的两条切线,切点分别是A、B,点C在⊙O上,若∠P=30°,则∠ACB=
如图,PA、PB是⊙O的两条切线,切点分别是A、B,点C在⊙O上,若∠P=30°,则∠ACB=考点:切线的性质,圆周角定理
专题:
分析:连接OA,OB,由切线的性质可得∠OBP=∠OAP=90°,由四边形的内角和为360°,可求∠O的度数,再根据圆周角定理求∠C的度数.
解答:
 解:连接OA,OB,
解:连接OA,OB,
∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,
即∠OBP=∠OAP=90°,
∵∠P=30°,四边形APBO的内角和为360°,
∴∠O=150°,
∴∠C=
∠O=
×150°=75°.
 解:连接OA,OB,
解:连接OA,OB,∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,
即∠OBP=∠OAP=90°,
∵∠P=30°,四边形APBO的内角和为360°,
∴∠O=150°,
∴∠C=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了切线的性质和圆周角定理,解题的关键是连接OA,OB,得出∠OBP和∠OAP是90°.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
在对某二次三项式进行因式分解,小明同学看错了二次项系数而将分解为8(x-1)(2x-1),小敏同学因看错了一次项系数而将其分解为2(x-1)(9x-4),求这个多项式,并将此多项式进行正确的因式分解.
下列运算正确的是( )
| A、a+a=a2 | ||
| B、(-a3)2=a5 | ||
C、(
| ||
| D、3a•a2=a3 |
已知点P位于y轴左侧,距y轴4个单位长度,位于x轴上方,距离x轴3个单位长度,则点P坐标是( )
| A、(-3,4) |
| B、(3,4) |
| C、(-4,3) |
| D、(4,3) |
 观察下图,在A、B、C、D四幅图案中,能通过图案平移得到的是( )
观察下图,在A、B、C、D四幅图案中,能通过图案平移得到的是( )A、 |
B、 |
C、 |
D、 |
若( )×(-2)=1,则括号内填一个实数应该是( )
A、-
| ||
| B、2 | ||
| C、-2 | ||
D、
|
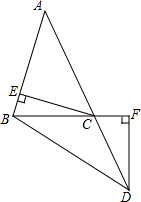 如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且CE=DF.
如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且CE=DF.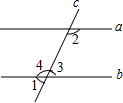 如图,先填空后证明.
如图,先填空后证明.