题目内容
12.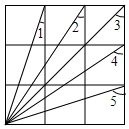 如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于225°.
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于225°.
分析 首先判定△ABC≌△AEF,△ABD≌△AEH,可得∠5=∠BCA,∠4=∠BDA,然后可得∠1+∠5=∠1+∠BCA=90°,∠2+∠4=∠2+∠BDA=90°,然后可得∠1+∠2+∠3+∠4+∠5的值.
解答 解:在△ABC和△AEF中,$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△AEF(SAS),
∴∠5=∠BCA,
∴∠1+∠5=∠1+∠BCA=90°,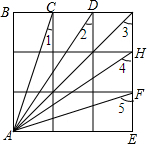
在△ABD和△AEH中,$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BD=HE}\end{array}\right.$,
∴△ABD≌△AEH(SAS),
∴∠4=∠BDA,
∴∠2+∠4=∠2+∠BDA=90°,
∵∠3=45°,
∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°.
故答案为:225°.
点评 此题主要考查了全等三角形的判定和性质,关键是掌握全等三角形的性质:全等三角形对应角相等.

练习册系列答案
相关题目
20.下列计算正确的是( )
| A. | 3-(2-3)=2 | B. | 2(2a-b)-3(b-2a)=10a-5b | ||
| C. | 6÷($\frac{1}{2}$-$\frac{1}{3}$)=12-18=-6 | D. | (-4)2-$\root{3}{-8}$=14 |
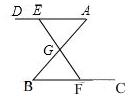 如图,在△ABC中,BC=4cm,过点A作射线AD∥BC,点E从点A出发沿射线AD以1cm/s的速度运动.同时点F从点B出发沿射线BC以1cm/s速度运动,连结EF交AB于点G,设点E运动时间为t(s).
如图,在△ABC中,BC=4cm,过点A作射线AD∥BC,点E从点A出发沿射线AD以1cm/s的速度运动.同时点F从点B出发沿射线BC以1cm/s速度运动,连结EF交AB于点G,设点E运动时间为t(s).
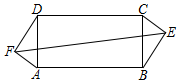 矩形ABCD中,AD=5,AB=10,E、F分别为矩形外的两点,BE=DF=4,AF=CE=3,则EF=$\sqrt{221}$.
矩形ABCD中,AD=5,AB=10,E、F分别为矩形外的两点,BE=DF=4,AF=CE=3,则EF=$\sqrt{221}$.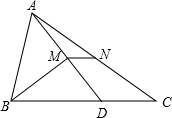 如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=9,则MN=2.
如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=9,则MN=2.