题目内容
菱形与正方形的形状有差异,我们将菱形与正方形的接近程度记为“接近度”.设菱形相邻的两个内角的度数分别为m°和n°,将菱形与正方形的“接近度”定义为|m-n|.在平面直角坐标系中,抛物线y=x2+
bx+c(b<0)交y轴于点A(与原点O不同),以AO为边作菱形OAPQ.
(1)当c=-
b时,抛物线上是否存在点P,使菱形OAPQ与正方形的“接近度”为0,请说明理由.
(2)当c>0时,对于任意的b,抛物线y=x2+
bx+c上是否存在点P,满足菱形OAPQ与正方形的“接近度”为60?若存在,请求出所有满足条件的b与c的关系式;若不存在,请说明理由.
| 3 |
(1)当c=-
| 3 |
(2)当c>0时,对于任意的b,抛物线y=x2+
| 3 |
考点:二次函数综合题
专题:压轴题
分析:(1)表示出点A的坐标,再根据正方形的四条边都相等且每一个角都是直角取点P的坐标,然后根据二次函数图象上点的坐标特征进行验证即可;
(2)根据“接近度”的定义求出m、n的值,然后分点P在y轴右侧时,∠OAP=120°和∠OAP=60°两种情况求出点P的坐标,再代入抛物线解析式求出b、c的关系式,然后根据b<0求出c的取值范围,进行验证即可;点P在y轴左侧时,只有∠OAP=120°,表示出点P的坐标,再代入抛物线解析式得到b、c的关系式,然后根据b<0求出c的取值范围,再进行验证.
(2)根据“接近度”的定义求出m、n的值,然后分点P在y轴右侧时,∠OAP=120°和∠OAP=60°两种情况求出点P的坐标,再代入抛物线解析式求出b、c的关系式,然后根据b<0求出c的取值范围,进行验证即可;点P在y轴左侧时,只有∠OAP=120°,表示出点P的坐标,再代入抛物线解析式得到b、c的关系式,然后根据b<0求出c的取值范围,再进行验证.
解答:(1)解:(1)存在.
当c=-
b时,点A的坐标为(0,-
b),
取P(-
b,-
b),
当x=-
b时,y=(-
b)2+
b×(-
b)-
b=-
b,
故点P在抛物线上,且OA=AP,OA⊥P,
∴m=n=90,
∴抛物线上存在点P,使菱形OAPQ与正方形的“接近度”为0;
(2)解:∵菱形OAPQ与正方形的“接近度”为60,
∴|m-n|=60,
又∵m+n=180,
∴m=120,n=60或m=60,n=120,
当P在y轴右侧时:①当∠OAP=120°时,P1(
c,
c)且在y=x2+
bx+c上,
∴(
c)2+
b×
c+c=
c,
∴b=
-
c,
∵b<0,
∴
-
c<0,
解得c>
,
即当c>
时,b与c的关系式为b=
-
c;
②当∠OAP=60°时,P2(
c,
c),且在y=x2+
bx+c上,
∴(
c)2+
b×
c+c=
c,
∴b=-
-
c,
∵b<0,
∴-
-
c<0,
解得c>-
,
举例:当b=-
时,c=-
<0,不满足对任意b,c>0,不符合题意;
当P在y轴左侧时:只可能存在∠OAP=120°,P3(-
c,
c)且在y=x2+
bx+c上,
∴(-
c)2+
b×(-
c)+c=
c,
∴b=
c-
,
∵b<0,
∴
c-
<0,
解得c<
,
举例:当b=-1时,c=-
,不满足对任意b,c>0,不符合题意;
综上所述,b与c的关系式为b=
-
c.
当c=-
| 3 |
| 3 |
取P(-
| 3 |
| 3 |
当x=-
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
故点P在抛物线上,且OA=AP,OA⊥P,
∴m=n=90,
∴抛物线上存在点P,使菱形OAPQ与正方形的“接近度”为0;
(2)解:∵菱形OAPQ与正方形的“接近度”为60,
∴|m-n|=60,

又∵m+n=180,
∴m=120,n=60或m=60,n=120,
当P在y轴右侧时:①当∠OAP=120°时,P1(
| ||
| 2 |
| 3 |
| 2 |
| 3 |
∴(
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴b=
| 1 |
| 3 |
| 1 |
| 2 |
∵b<0,
∴
| 1 |
| 3 |
| 1 |
| 2 |
解得c>
| 2 |
| 3 |
即当c>
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
②当∠OAP=60°时,P2(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴(
| ||
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴b=-
| 1 |
| 3 |
| 1 |
| 2 |
∵b<0,
∴-
| 1 |
| 3 |
| 1 |
| 2 |
解得c>-
| 2 |
| 3 |
举例:当b=-
| 1 |
| 6 |
| 1 |
| 3 |
当P在y轴左侧时:只可能存在∠OAP=120°,P3(-
| ||
| 2 |
| 3 |
| 2 |
| 3 |
∴(-
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴b=
| 1 |
| 2 |
| 1 |
| 3 |
∵b<0,
∴
| 1 |
| 2 |
| 1 |
| 3 |
解得c<
| 2 |
| 3 |
举例:当b=-1时,c=-
| 4 |
| 3 |
综上所述,b与c的关系式为b=
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题是二次函数综合题型,主要利用了正方形的性质,二次函数图象上点的坐标特征,难点在于(2)分情况讨论并根据b是负数求出c必须是正数关系式才成立.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 已知如图,菱形ABCD中,∠ADC=120°,AC=12
已知如图,菱形ABCD中,∠ADC=120°,AC=12 如图,已知∠A=∠D,∠ABC=∠DCB,求证:AC=DB.
如图,已知∠A=∠D,∠ABC=∠DCB,求证:AC=DB.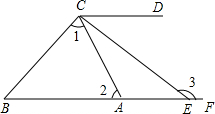 如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E. 如图,在正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:
如图,在正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:
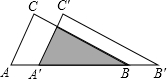 如图,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=
如图,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=