题目内容
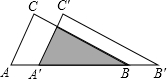如图，把△ABC沿AB边平移到△A′B′C′的位置，它们的重叠部分（即图中的阴影部分）的面积是△ABC的面积的一半，若AB=| 2 |
考点：相似三角形的判定与性质,平移的性质
专题：
分析：利用相似三角形面积的比等于相似比的平方先求出A′B，再求AA′就可以了．
解答：解：设BC与A′C′交于点E，
由平移的性质知，AC∥A′C′，
∴△BEA′∽△BCA，
∴S△BEA′：S△BCA=A′B2：AB2=1：2，
∵AB=
，
∴A′B=1，
∴AA′=AB-A′B=
-1，
故答案为：
-1．
由平移的性质知，AC∥A′C′，
∴△BEA′∽△BCA，
∴S△BEA′：S△BCA=A′B2：AB2=1：2，
∵AB=
| 2 |
∴A′B=1，
∴AA′=AB-A′B=
| 2 |
故答案为：
| 2 |
点评：本题利用了相似三角形的判定和性质及平移的性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．
练习册系列答案
相关题目
如图，在菱形ABCD中，∠ABC=120°，E是AB边上的中点，P是AC边上一动点，PB+PE的最小值是