题目内容
6．
如图?ABCD，E是BC上一点，BE：EC=2：3，AE交BD于F，则BF：FD等于（ ）| A． | 2：5 | B． | 3：5 | C． | 2：3 | D． | 5：7 |
分析 由在?ABCD中，且BE：EC=2：3，易得BE：AD=2：5，△ADF∽△EBF，然后根据相似三角形的对应边成比例，即可求得答案．
解答 解：∵BE：EC=2：3，
∴BE：BC=2：5，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴BE：AD=2：5，△ADF∽△EBF，
∴$\frac{BF}{FD}$=$\frac{BE}{AD}$=$\frac{2}{5}$．
故选D．
点评 此题考查了平行四边形的性质，相似三角形的判定与性质．此题难度不大，解题的关键是注意数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
4．若x+$\frac{1}{x}$=2，则$\frac{x^2}{{{x^4}+2{x^2}+1}}$的值是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{10}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
17．
如图，点B，C，D在同一直线上，则∠1，∠2，∠3的大小关系是（ ）
如图，点B，C，D在同一直线上，则∠1，∠2，∠3的大小关系是（ ）| A． | ∠1＜∠2＜∠3 | B． | ∠1＜∠3＜∠2 | C． | ∠2＜∠3＜∠1 | D． | ∠3＜∠2＜∠1 |
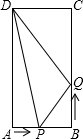如图，在矩形ABCD中，AB=6cm，BC=12cm，点P沿边AB从点A向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，设点P、Q移动的时间为t s．问：
如图，点E、F在AC上，AB∥CD，AB=CD，AE=CF．求证：
如图，已知DE=CE，∠1=∠2，求证：∠3=∠4．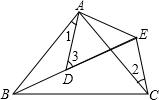
如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=35°，则∠3=60°．
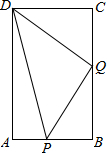如图，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，设运动的时间为t秒，有一点到终点运动即停止．问：是否存在这样的时刻，使S△DPQ=28cm2？若存在，请求出t的值；若不存在，请说明理由．