题目内容
18.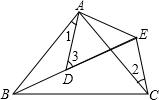 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=35°,则∠3=60°.
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=35°,则∠3=60°.
分析 由△BAD≌△CAE,推出∠ABD=∠2=35°,推出∠3=∠1+∠ABD=∠1+∠2=25°+35°=60°即可.
解答 证明:在△BAD和△CAE中,
$\left\{\begin{array}{l}{BA=CA}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE,
∴∠ABD=∠2=35°,
∴∠3=∠1+∠ABD=∠1+∠2=25°+35°=60°.
故答案为60°.
点评 本题考查全等三角形的判定和性质,三角形的外角的性质等知识,解题的关键是灵活运用所学知识,属于中考常考题型.

练习册系列答案
相关题目
16.方程x2+3x-6=0与x2-6x+3=0所有根的乘积等于( )
| A. | -18 | B. | -3 | C. | 3 | D. | 18 |
6. 如图?ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )
如图?ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )
 如图?ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )
如图?ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )| A. | 2:5 | B. | 3:5 | C. | 2:3 | D. | 5:7 |

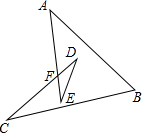 如图,求∠A+∠B+∠C+∠D+∠E的度数:180°.
如图,求∠A+∠B+∠C+∠D+∠E的度数:180°.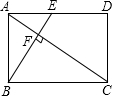 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )