题目内容
1.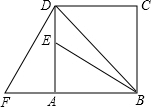 四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,∠F=60°,求:
四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,∠F=60°,求:(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.
分析 (1)由于△ADF旋转一定角度后得到△ABE,根据旋转的性质得到旋转中心为点A,∠DAB等于旋转角,于是得到旋转角为90°;
(2)根据旋转的性质得到AE=AF=4,∠AEB=∠F=60°,则∠ABE=90°-60°=30°,解直角三角形得到AD=4$\sqrt{3}$,∠ABD=45°,所以DE=4$\sqrt{3}$-4,然后利用∠EBD=∠ABD-∠ABE计算即可.
解答 解:(1)∵△ADF旋转一定角度后得到△ABE,
∴旋转中心为点A,∠DAB等于旋转角,
∴旋转角为90°;
(2)∵△ADF以点A为旋转轴心,顺时针旋转90°后得到△ABE,
∴AE=AF=4,∠AEB=∠F=60°,
∴∠ABE=90°-60°=30°,
∵四边形ABCD为正方形,
∴AD=AB=4$\sqrt{3}$,∠ABD=45°,
∴DE=4$\sqrt{3}$-4,
∠EBD=∠ABD-∠ABE=15°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.方程2(2x+1)(x-3)=0的两根分别为( )
| A. | $\frac{1}{2}$和3 | B. | -$\frac{1}{2}$和3 | C. | $\frac{1}{2}$和-3 | D. | -$\frac{1}{2}$和-3 |
16.下列长度的三条线段,能组成三角形的是( )
| A. | 3,4,8 | B. | 5,6,11 | C. | 6,8,16 | D. | 5,6,10 |
10.在下面四个立体图形中,从左面看与从正面看所得到的平面图形不相同的是( )
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
 已知一次函数y=kx+b的图象经过点(1,2),(0,4).
已知一次函数y=kx+b的图象经过点(1,2),(0,4). 如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC
如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC