题目内容
10.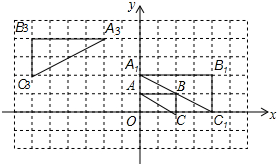 如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.
如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.(1)△ABC与△A1B1C1的位似比等于$\frac{1}{2}$;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为(-2x-2,2y+2).
分析 (1)根据位似图形可得位似比即可;
(2)根据轴对称图形的画法画出图形即可;
(3)根据△A3B3C3与△A2B2C2的关系过程其变化过程即可;
(4)根据三次变换规律得出坐标即可.
解答 解:(1))△ABC与△A1B1C1的位似比等于=$\frac{AB}{{A}_{1}{B}_{1}}=\frac{2}{4}=\frac{1}{2}$;
(2)如图所示
(3)△A3B3C3是由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;
(4)点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为(-2x-2,2y+2).
故答案为:$\frac{1}{2}$;(-2x-2,2y+2).
点评 此题考查作图问题,关键是根据轴对称图形的画法和位似图形的性质分析.

练习册系列答案
相关题目
1.在△ABC中,D、E分别为AB、AC边上中点,且DE=6,则BC的长度是( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
18.直线y=x+b(b>0)与直线y=kx(k<0)的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.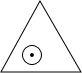 如图,一个半径为1的圆形纸片在边长为a(a≥2$\sqrt{3}$)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
如图,一个半径为1的圆形纸片在边长为a(a≥2$\sqrt{3}$)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
 如图,一个半径为1的圆形纸片在边长为a(a≥2$\sqrt{3}$)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
如图,一个半径为1的圆形纸片在边长为a(a≥2$\sqrt{3}$)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )| A. | $\frac{π}{3}$ | B. | $\frac{3\sqrt{3}-π}{3}$ | C. | 3$\sqrt{3}$-π | D. | 不能求出具体值 |
 如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2$\sqrt{3}$,则阴影部分的面积为2π-3$\sqrt{3}$.
如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2$\sqrt{3}$,则阴影部分的面积为2π-3$\sqrt{3}$.