题目内容
20.已知抛物线y=ax2-2ax与直线l:y=ax(a>0)的交点除了原点外,还相交于另一点A.(1)分别求出这个抛物线的顶点,点A的坐标(可用含a的式子表示);
(2)将抛物线y=ax2-2ax沿着x轴对折(旋转180°)后,得到的图象叫做“新抛物线”,当a=1时,求这个“新抛物线”的解析式,并判断这个“新抛物线”的顶点是否在直线l上.
分析 (1)由y=ax2-2ax=a(x-1)2-a,即可求得这个抛物线的顶点坐标,又由y=ax2-2ax与y=ax(a>0)可得抛物线和直线的交点坐标为(0,0)、(3,3a),即可求得点A的坐标;
(2)存在.首先求得原抛物线为y=x2-2x,可得新抛物线为y=-x2+2x,直线l:x-y=0.把新抛物线的顶点坐标代入直线l进行验证即可.
解答  解:(1)∵y=ax2-2ax=a(x-1)2-a,
解:(1)∵y=ax2-2ax=a(x-1)2-a,
∴抛物线的顶点坐标为(1,-a),
由y=ax2-2ax与y=ax(a>0)可得抛物线和直线的交点坐标为(0,0)、(3,3a),
∴A点坐标为(3,3a);
(2)∴当a=1时,A坐标为(3,3),
∴OA=3$\sqrt{2}$,
∴原抛物线为y=x2-2x,则新抛物线为y=-x2+2x=-(x-1)2+1,其顶点坐标是(1,1).
把点(1,1)直线l:y=x,得
1=1.
即这个“新抛物线”的顶点在直线l上.
点评 此题考查了二次函数的顶点坐标的求法,二次函数与一次函数的交点坐标问题,以及线段的长的求解方法等知识.此题综合性很强,难度较大,注意解题的关键是方程思想的应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5吨,5辆大货车与6辆小货车一次可以运货35吨.设一辆大货车一次可以运货x吨,一辆小货车一次可以运货y吨,根据题意所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{2x+3y=15.5}\\{5x+6y=35}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=35}\\{5x+6y=15.5}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+2y=15.5}\\{5x+6y=35}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+3y=15.5}\\{6x+5y=35}\end{array}\right.$ |
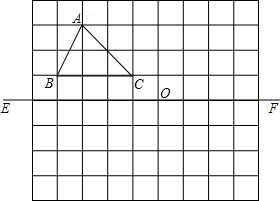 如图的小方格都是边长为1个单位的正方形,按照下列要去作图,(不写作法,只作出图形即可)
如图的小方格都是边长为1个单位的正方形,按照下列要去作图,(不写作法,只作出图形即可)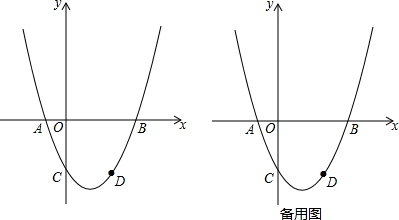
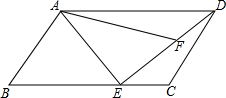 如图所示,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE;
如图所示,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE;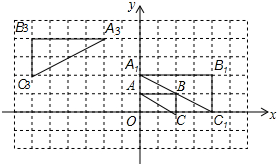 如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.
如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.