题目内容
13. 已知反比例函数y=$\frac{6}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB且AO=AB,则S△AOB=6.
已知反比例函数y=$\frac{6}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB且AO=AB,则S△AOB=6.
分析 根据等腰三角形的性质得出CO=BC,再利用反比例函数系数k的几何意义得出S△AOB即可.
解答  解:过点A作AC⊥OB于点C,
解:过点A作AC⊥OB于点C,
∵AO=AB,
∴CO=BC,
∵点A在其图象上,
∴$\frac{1}{2}$AC×CO=3,
∴$\frac{1}{2}$AC×BC=3,
∴S△AOB=6.
故答案为:6.
点评 此题主要考查了反比例函数图象上点的坐标特征,等腰三角形的性质以及反比例函数系数k的几何意义,正确分割△AOB是解题关键.

练习册系列答案
相关题目
4. 如图是一个风筝设计图,其主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,且AB≠AD,则下列判断不正确的是( )
如图是一个风筝设计图,其主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,且AB≠AD,则下列判断不正确的是( )
 如图是一个风筝设计图,其主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,且AB≠AD,则下列判断不正确的是( )
如图是一个风筝设计图,其主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,且AB≠AD,则下列判断不正确的是( )| A. | AC垂直平分BD | B. | △ABD≌△CBD | C. | △AOB≌△COB | D. | △AOD≌△COD |
1.下列根式中,不能再化简的二次根式是( )
| A. | $\sqrt{{a^2}+1}$ | B. | -$\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{27}$ |
8.下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. | 正三角形 | B. | 平行四边形 | C. | 五角星 | D. | 矩形 |
5. 如图,AD是△ABC的一条中线,CE是△ACD的一条中线,S△AEC=1,则S△ABC=( )
如图,AD是△ABC的一条中线,CE是△ACD的一条中线,S△AEC=1,则S△ABC=( )
 如图,AD是△ABC的一条中线,CE是△ACD的一条中线,S△AEC=1,则S△ABC=( )
如图,AD是△ABC的一条中线,CE是△ACD的一条中线,S△AEC=1,则S△ABC=( )| A. | 2 | B. | 3 | C. | 4 | D. | 无法计算 |
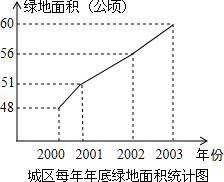 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).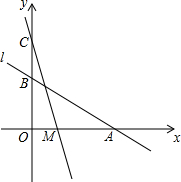 如图,直线L:y=-$\frac{1}{2}x+2$与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}x+2$与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.