题目内容
18.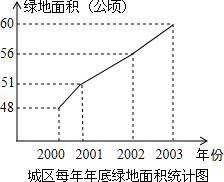 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).(1)根据图中所提供的信息回答下列问题:2003年底的绿地面积为60公顷,比2002年底增加了4公顷;在2001年,2002年,2003年这三年中,绿地面积增加最多的是2002年;
(2)为满足城市发展的需要,计划到2005年底使城区绿地面积达到72.6公顷,试求今明两绿地面积的年平均增长率.
分析 (1)根据统计图能看出2003年的绿化面积和2002年的绿化面积.
(2)设04,05两年绿地面积的年平均增长率为x,根据计划到2005年底使城区绿地面积达到72.6公顷,可列方程求解.
解答 解:(1)2003年的绿化面积为60公顷,2002年绿化的面积为56公顷.
60-56=4,比2002年底增加了4公顷,这三年中增长最多的是2002年.
(2)设04,05两年绿地面积的年平均增长率为x,依题意有
60(1+x)2=72.6.
x=10%或x=-210%(舍去).
答:04,05两年绿地面积的年平均增长率10%.
点评 本题考查折线统计图及一元二次方程的应用的知识,从上面可看出每年对应的公顷数,以及2003年和2005年的公顷数,求出增长率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列说法正确的是( )
| A. | 等弧所对的圆心角相等 | |
| B. | 三角形的外心到这个三角形的三边距离相等 | |
| C. | 经过三点可以作一个圆 | |
| D. | 相等的圆心角所对的弧相等 |
6.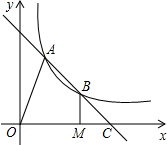 如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )
如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )
 如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )
如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7.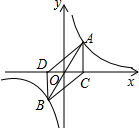 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )| A. | S=2 | B. | 2<S<4 | C. | S=4 | D. | S>4 |
 已知反比例函数y=$\frac{6}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB且AO=AB,则S△AOB=6.
已知反比例函数y=$\frac{6}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB且AO=AB,则S△AOB=6.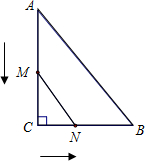 已知:如图,在Rt△ABC中,∠ACB=90°,BC=6cm,AB=10cm.一动点M在边AC上从A向C以3cm/s的速度匀速运动,另一动点N在边BC上同时从C向B以2cm/s的速度匀速运动,当其中一个点到达终点时另一点也随之停止运动.设运动的时间为x秒.
已知:如图,在Rt△ABC中,∠ACB=90°,BC=6cm,AB=10cm.一动点M在边AC上从A向C以3cm/s的速度匀速运动,另一动点N在边BC上同时从C向B以2cm/s的速度匀速运动,当其中一个点到达终点时另一点也随之停止运动.设运动的时间为x秒.