题目内容
19.解下列方程:(1)x2+2x-2=0(用配方法解)
(2)3x2-7x+4=0
(3)$\frac{2x}{x-2}$-$\frac{2}{2-x}$=1.
分析 (1)移项,配方,开方,即可得出两个方程,求出方程的解即可;
(2)分解因式,即可得出两个方程,求出方程的解即可;
(3)先把分式方程转化成整式方程,求出方程的解,最后进行检验即可.
解答 解:(1)x2+2x-2=0,
x2+2x=2,
x2+2x+1=3,
(x+1)2=3,
开方得:x+1=$±\sqrt{3}$,
x1=-1+$\sqrt{3}$,x2=-1-$\sqrt{3}$;
(2)3x2-7x+4=0,
(3x-4)(x-1)=0,
3x-4=0,x-1=0,
x1=$\frac{4}{3}$,x2=-1;
(3)方程两边都乘以x-2得:2x+2=x-2,
解得:x=-4,
检验:当x=-4时,x-2≠0,
所以x=-4是原方程的解,
即原方程的解为x=-4.
点评 本题考查了解一元二次方程和解分式方程等知识点,能选择适当的方法解一元二次方程是解(1)(2)的关键,能把分式方程转化成整式方程是解(3)的关键.

练习册系列答案
相关题目
10.关于x的方程2x-m=1的解是x=3,则m的值为( )
| A. | 5 | B. | -5 | C. | 7 | D. | -7 |
7.下列条件中,能判定四边形是平行四边形的是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 对角线互相垂直且相等 |
6.在数-3,2,-4中任取两个数相乘,其中积最小的是( )
| A. | -6 | B. | -12 | C. | -8 | D. | 12 |
7.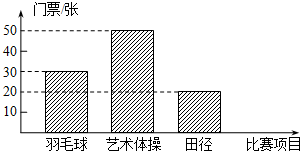 2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.
2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.
依据上面的表和图,回答下列问题:
(1)其中观看羽毛球比赛的门票有张;观看田径比赛的门票占全部门票的;
(2)公司决定采用随机抽取的方式把门票分别配给部分员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小丽抽到艺术体操门票的概率是$\frac{1}{2}$;
(3)若该公司购买全部门票共花36000元,试求每张田径门票的价格.
 2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.
2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.| 比赛项目 | 票价(元/张) |
| 羽毛球 | 400 |
| 艺术体操 | 240 |
| 田径 | x |
(1)其中观看羽毛球比赛的门票有张;观看田径比赛的门票占全部门票的;
(2)公司决定采用随机抽取的方式把门票分别配给部分员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小丽抽到艺术体操门票的概率是$\frac{1}{2}$;
(3)若该公司购买全部门票共花36000元,试求每张田径门票的价格.
 如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.