题目内容
11.先化简($\frac{{x}^{2}-2x+4}{x-1}$+2-x)÷$\frac{{x}^{2}-4}{1-x}$,再在-2,0,1,2中选一个合适的数代入求值.分析 先化简分式,然后根据分式有意义的条件即可求出答案
解答 解:原式=$\frac{{x}^{2}-2x+4+2x-{x}^{2}-2+x}{x-1}$•$\frac{1-x}{{x}^{2}-4}$
=$\frac{x+2}{x-1}$•$\frac{-(x-1)}{(x+2)(x-2)}$
=-$\frac{1}{x-2}$
∵$\left\{\begin{array}{l}{x-1≠0}\\{{x}^{2}-4≠0}\end{array}\right.$
∴x≠1且x≠±2
∴x只能取0,
∴原式=$\frac{1}{2}$
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列图形中,不是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.估计$\sqrt{3}$+1的值在( )
| A. | 2和3之间 | B. | 3和4 之间 | C. | 4和5之间 | D. | 5和6之间 |
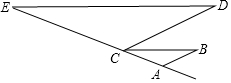 已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA
已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA
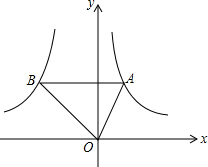 如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B,且S△AOB=5.
如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B,且S△AOB=5.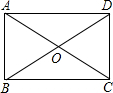 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=1,则AD的长为$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=1,则AD的长为$\sqrt{3}$.