题目内容
 如图,在△ABC中,∠BAC=60°,在△ABC的内部取一点O,连接OA,OB,OC,恰有OA=OC,∠OBA=20°,∠OCA=40°.①∠BOA=140°;②△OAB是等腰三角形;③∠OBC=30°;④△OBC是等腰三角形;⑤△ABC是等边三角形,则以上说法中正确的是( )
如图,在△ABC中,∠BAC=60°,在△ABC的内部取一点O,连接OA,OB,OC,恰有OA=OC,∠OBA=20°,∠OCA=40°.①∠BOA=140°;②△OAB是等腰三角形;③∠OBC=30°;④△OBC是等腰三角形;⑤△ABC是等边三角形,则以上说法中正确的是( )| A、①②③④⑤ | B、①②③④ |
| C、①②③⑤ | D、①②④ |
考点:等腰三角形的判定,等边三角形的判定
专题:
分析:根据等腰三角形性质求出∠OAC=40°,求出∠BAO=20°,推出OA=OB=OC,根据等腰三角形性质求出∠OBC=∠OCB=30°,判断各个选项即可.
解答:解:∵∠OCA=40°,OA=OC,
∴∠OAC=∠OCA=40°,
∵∠BAC=60°,
∴∠OAB=60°-40°=20°,
∵∠OBA=20°,
∴OB=OA,∠AOB=180°-20°-20°=140°,∴①②正确;
∵∠BAC=60°,∠OBA=20°,∠OCA=40°,
∴∠OBC+∠OCB=60°,
∵OA=OB,OA=OC,
∴OB=OC,
∴∠OBC=∠OCB=30°,∴③④正确;
∵∠ABC=20°+30°=50°,∠ACB=30°+40°=70°,∠BAC=60°,
∴△ABC不是等边三角形,∴⑤错误;
故选B.
∴∠OAC=∠OCA=40°,
∵∠BAC=60°,
∴∠OAB=60°-40°=20°,
∵∠OBA=20°,
∴OB=OA,∠AOB=180°-20°-20°=140°,∴①②正确;
∵∠BAC=60°,∠OBA=20°,∠OCA=40°,
∴∠OBC+∠OCB=60°,
∵OA=OB,OA=OC,
∴OB=OC,
∴∠OBC=∠OCB=30°,∴③④正确;
∵∠ABC=20°+30°=50°,∠ACB=30°+40°=70°,∠BAC=60°,
∴△ABC不是等边三角形,∴⑤错误;
故选B.
点评:本题考查了等边三角形的判定,三角形内角和定理,等腰三角形的性质的应用,解此题的关键是求出各个角的度数和得出OA=OB=OC.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
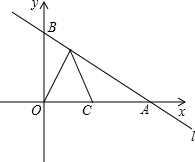 如图所示,在平面直角坐标系中,过B的直线l:y=kx+1与x轴交于A点,且∠BAO=30°.
如图所示,在平面直角坐标系中,过B的直线l:y=kx+1与x轴交于A点,且∠BAO=30°.