题目内容
 如图,△ABC是等边三角形,D是BC上一点,AB=8,BD=3,将△ABD饶点A逆时针旋转60°到△ACE的位置,连接DE,则DE的长为
如图,△ABC是等边三角形,D是BC上一点,AB=8,BD=3,将△ABD饶点A逆时针旋转60°到△ACE的位置,连接DE,则DE的长为考点:旋转的性质,等边三角形的判定与性质
专题:计算题
分析:作DH⊥AB于H,由△ABC是等边三角形得∠B=60°,则在Rt△BDH中,根据含30度的直角三角形三边的关系计算得BH=
BD=
,DH=
BH=
,则AH=AB-BH=
,再利用勾股定理计算出AD=7,然后根据旋转的性质得AD=AE,∠DAE=60°,则可判断△DAE为等边三角形,于是利用等边三角形的性质易得DE=7.
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
3
| ||
| 2 |
| 13 |
| 2 |
解答:解: 作DH⊥AB于H,
作DH⊥AB于H,
∵△ABC是等边三角形,
∴∠B=60°,
在Rt△BDH中,∵∠BDH=30°,
∴BH=
BD=
,DH=
BH=
,
∴AH=AB-BH=8-
=
,
在Rt△AHD中,∵DH=
,AH=
,
∴AD=
=7,
∵△ABD饶点A逆时针旋转60°到△ACE的位置,
∴AD=AE,∠DAE=60°,
∴△DAE为等边三角形,
∴DE=AD=7.
故答案为7.
 作DH⊥AB于H,
作DH⊥AB于H,∵△ABC是等边三角形,
∴∠B=60°,
在Rt△BDH中,∵∠BDH=30°,
∴BH=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
3
| ||
| 2 |
∴AH=AB-BH=8-
| 3 |
| 2 |
| 13 |
| 2 |
在Rt△AHD中,∵DH=
3
| ||
| 2 |
| 13 |
| 2 |
∴AD=
| DH2+AH2 |
∵△ABD饶点A逆时针旋转60°到△ACE的位置,
∴AD=AE,∠DAE=60°,
∴△DAE为等边三角形,
∴DE=AD=7.
故答案为7.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
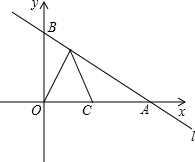 如图所示,在平面直角坐标系中,过B的直线l:y=kx+1与x轴交于A点,且∠BAO=30°.
如图所示,在平面直角坐标系中,过B的直线l:y=kx+1与x轴交于A点,且∠BAO=30°. 如图,在长方形的台球桌面上,选择适当的角度打击白球,可以使白球经过两次反弹后将黑球直接撞入袋中,此时∠1=∠2,∠3=∠4,并且∠2+∠3=90°,∠4+∠5=90°.如果黑球与洞口的连线和台球桌面边缘的夹角∠5=40°,那么∠1应该等于多少度才能保证黑球准确入袋?请说明理由.
如图,在长方形的台球桌面上,选择适当的角度打击白球,可以使白球经过两次反弹后将黑球直接撞入袋中,此时∠1=∠2,∠3=∠4,并且∠2+∠3=90°,∠4+∠5=90°.如果黑球与洞口的连线和台球桌面边缘的夹角∠5=40°,那么∠1应该等于多少度才能保证黑球准确入袋?请说明理由.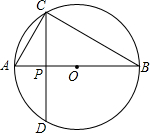 如图所示,点C在以AB为直径的⊙O上,CD⊥AB于点P.求当AP=
如图所示,点C在以AB为直径的⊙O上,CD⊥AB于点P.求当AP=