题目内容
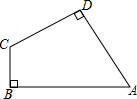如图，在四边形ABCD中，∠A=60°，∠B=∠D=90°，AD=3，BC=2．求AB的长．考点：勾股定理,含30度角的直角三角形
专题：
分析：延长DC交AB的延长线于点E，根据∠D=90°，∠A=60°可知AE=2AD=6，CE=2BC=4，再根据勾股定理求出BE的长，根据AB=AE-BE即可得出结论．
解答：
解：延长DC交AB的延长线于点E，
∵∠B=∠D=90°，∠A=60°，AD=3，BC=2，
∴∠E=30°，
∴AE=2AD=6，CE=2BC=4，
∴BE=
=
=2
，
∴AB=AE-BE=6-2
．
解：延长DC交AB的延长线于点E，∵∠B=∠D=90°，∠A=60°，AD=3，BC=2，
∴∠E=30°，
∴AE=2AD=6，CE=2BC=4，
∴BE=
| CE2-BC2 |
| 42-22 |
| 3 |
∴AB=AE-BE=6-2
| 3 |
点评：本题考查的是勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
如图，△ABC内接于⊙O，AB=8，AC=5，高AD=4，求⊙O的直径．
已知：如图，∠1=∠2，CE∥BF，试说明：AB∥CD．
一副三角板如图摆放，点F是45°角三角板ABC的斜边的中点，AC=4．当30°角三角板DEF的直角顶点绕着点F旋转时，直角边DF，EF分别与AC，BC相交于点M，N．在旋转过程中有以下结论：