题目内容
 一副三角板如图摆放,点F是45°角三角板ABC的斜边的中点,AC=4.当30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点M,N.在旋转过程中有以下结论:
一副三角板如图摆放,点F是45°角三角板ABC的斜边的中点,AC=4.当30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点M,N.在旋转过程中有以下结论:①MF=NF;
②四边形CMFN的面积保持不变;
③MN长度的最小值为2;
④以AM、BN、MN的长为边的三角形是直角三角形,
其中正确的结论是
考点:旋转的性质,全等三角形的判定与性质,勾股定理的逆定理
专题:计算题
分析:连结CF,如图,根据等腰直角三角形的性质和直角三角形斜边上的中线性质得到CF=BF,CF平分∠ACB,CF⊥AB,∠B=45°,则∠ACF=45°,∠2+∠3=45°,利用等角的余角相等可得∠1=∠3,则可根据“ASA”判断△CFM≌△BFN,则MF=NF;由△CFM≌△BFN得到S△CFM=S△BFN,所以S四边形CMFN=S△BFC=
S△ACB=4;易得△MFN为等腰直角三角形,则MN=
FM,当FM⊥AC时,根据垂相等最短得到FM最小,此时MN最小,利用△ACF为等腰直角三角形,即可得到当FM⊥AC时,FM=
AC=2,于是得到MN长度的最小值为2
;由△CFM≌△BFN得到CM=BN,同理可证明△CFN≌△AFM得到CN=AM,利用CN2+CM2=MN2得到AM2+BN2=MN2,于是根据勾股定理的逆定理即可判断以AM、BN、MN的长为边的三角形是直角三角形,所以④正确.
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
解答:解:连结CF,如图,
∵点F是45°角三角板ABC的斜边的中点,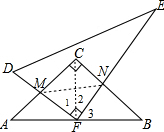
∴CF=BF,CF平分∠ACB,CF⊥AB,∠B=45°,
∴∠ACF=45°,∠2+∠3=45°
∵∠1+∠2=90°,
∴∠1=∠3,
在△CFM和△BFN中,
,
∴△CFM≌△BFN(ASA),
∴MF=NF,所以①正确;
∵△CFM≌△BFN,
∴S△CFM=S△BFN,
∴S四边形CMFN=S△BFC=
S△ACB=
×
×4×4=4,所以②正确;
∵MF=NF,∠MFN=90°,
∴△MFN为等腰直角三角形,
∴MN=
FM,
当FM⊥AC时,FM最小,此时MN最小,
∵△ACF为等腰直角三角形,
∴当FM⊥AC时,FM=
AC=2,
∴MN长度的最小值为2
,所以③错误;
∵△CFM≌△BFN,
∴CM=BN,
同理可证明△CFN≌△AFM,
∴CN=AM,
在Rt△CMN中,CN2+CM2=MN2,
∴AM2+BN2=MN2,
∴以AM、BN、MN的长为边的三角形是直角三角形,所以④正确.
故答案为①②④.
∵点F是45°角三角板ABC的斜边的中点,

∴CF=BF,CF平分∠ACB,CF⊥AB,∠B=45°,
∴∠ACF=45°,∠2+∠3=45°
∵∠1+∠2=90°,
∴∠1=∠3,
在△CFM和△BFN中,
|
∴△CFM≌△BFN(ASA),
∴MF=NF,所以①正确;
∵△CFM≌△BFN,
∴S△CFM=S△BFN,
∴S四边形CMFN=S△BFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵MF=NF,∠MFN=90°,
∴△MFN为等腰直角三角形,
∴MN=
| 2 |
当FM⊥AC时,FM最小,此时MN最小,
∵△ACF为等腰直角三角形,
∴当FM⊥AC时,FM=
| 1 |
| 2 |
∴MN长度的最小值为2
| 2 |
∵△CFM≌△BFN,
∴CM=BN,
同理可证明△CFN≌△AFM,
∴CN=AM,
在Rt△CMN中,CN2+CM2=MN2,
∴AM2+BN2=MN2,
∴以AM、BN、MN的长为边的三角形是直角三角形,所以④正确.
故答案为①②④.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质和全等三角形的判定与性质;第④个结论需要运用勾股定理的逆定理进行判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
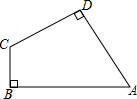 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=3,BC=2.求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=3,BC=2.求AB的长.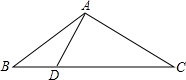 如图△ABC中,AB=AC=20,BC=32,D是BC上一点,且AD⊥AC,求BD的长.
如图△ABC中,AB=AC=20,BC=32,D是BC上一点,且AD⊥AC,求BD的长. 如图,在平面直角坐标系中,直线l:y=-
如图,在平面直角坐标系中,直线l:y=-