题目内容
有位财主临终前将一块平行四边形的田地分给两个儿子,如图①,O为田中一口井,他决定把相对的两块三角形的田地(△AOB、△COD)给大儿子,剩下的全部给小儿子,这口井两家何用.遗嘱公布之后,亲友们议论纷纷,有的说这样太不公平.聪明的同学,你认为这样公平吗?如图②,你能否找到一个简捷方法,将这块地分成两块,两个儿子分得的地一样大,而且公用这口井?


考点:平行四边形的性质
专题:应用题
分析:过O作GH⊥AD交AD于H,交BC于G,根据三角形的面积公式求出△AOD和△COB的面积之和等于
AD×GH,再根据平行四边形的面积即可求出答案.
| 1 |
| 2 |
解答: 解:公平,
解:公平,
理由是:过O作GH⊥AD交AD于H,交BC于G,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵GH⊥AD,
∴GH⊥BC,
∴阴影部分的面积是S△OAD+S△OBC=
AD×OH+
BC×OG=
AD×GH=
S平行四边形ABCD,
∴△AOD和△COB的面积之和等于平行四边形ABCD的面积的一半;
如图②,作出平行四边形的两条对角线,过对角线的交点和O点的直线能将平行四边形平分.
 解:公平,
解:公平,理由是:过O作GH⊥AD交AD于H,交BC于G,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵GH⊥AD,
∴GH⊥BC,
∴阴影部分的面积是S△OAD+S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△AOD和△COB的面积之和等于平行四边形ABCD的面积的一半;
如图②,作出平行四边形的两条对角线,过对角线的交点和O点的直线能将平行四边形平分.
点评:本题考查了平行四边形的性质,三角形的面积的应用,关键是根据题意求出阴影部分的面积等于平行四边形ABCD的面积的一半,题目较好,主要培养了学生运用所学的数学知识解决实际问题的能力.

练习册系列答案
相关题目
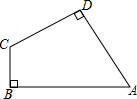 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=3,BC=2.求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=3,BC=2.求AB的长. 如图,在平面直角坐标系中,直线l:y=-
如图,在平面直角坐标系中,直线l:y=- 在四边形ABCD中,AB=2,BC=
在四边形ABCD中,AB=2,BC=