题目内容
二次函数y=ax2(a≠0)的图象经过点(-1,4)与一次函数y=ax+8的图象的交点为A、B.
(1)求出a的值,并写出二次函数,一次函数的解析式;
(2)求出这个二次函数的顶点坐标,对称轴,开口方向;
(3)求△AOB的面积.
(1)求出a的值,并写出二次函数,一次函数的解析式;
(2)求出这个二次函数的顶点坐标,对称轴,开口方向;
(3)求△AOB的面积.
考点:待定系数法求二次函数解析式,待定系数法求一次函数解析式,二次函数的性质
专题:计算题
分析:(1)把(-1,4)代入二次函数解析式求出a的值,确定出二次函数解析式与一次函数解析式即可;
(2)利用二次函数的性质求出顶点坐标,对称轴,以及开口方向即可;
(3)求出A与B的坐标,确定出三角形AOB面积即可.
(2)利用二次函数的性质求出顶点坐标,对称轴,以及开口方向即可;
(3)求出A与B的坐标,确定出三角形AOB面积即可.
解答:解:(1)把(-1,4)代入y=ax2,得:a=4,
故二次函数解析式为:y=4x2;一次函数解析式为y=4x+8;
(2)二次函数顶点坐标为(0,0),对称轴为y轴,开口方向向上;
(3)联立得:
,
消去y得:x2-x-2=0,即(x-2)(x+1)=0,
解得:x=2或x=-1,
把x=2代入得:y=16;把x=-1代入得:y=4,
则A(2,16),B(-1,4),
设直线AB解析式为y=mx+n,
把A与B坐标代入得:
,
解得:
,
故直线AB解析式为y=4x+8,
令x=0,得到y=8,即直线AB与y轴交点坐标为(0,8),
则S△AOB=
×8×|-1|+
×8×2=4+8=12.
故二次函数解析式为:y=4x2;一次函数解析式为y=4x+8;
(2)二次函数顶点坐标为(0,0),对称轴为y轴,开口方向向上;
(3)联立得:
|
消去y得:x2-x-2=0,即(x-2)(x+1)=0,
解得:x=2或x=-1,
把x=2代入得:y=16;把x=-1代入得:y=4,
则A(2,16),B(-1,4),
设直线AB解析式为y=mx+n,
把A与B坐标代入得:
|
解得:
|
故直线AB解析式为y=4x+8,
令x=0,得到y=8,即直线AB与y轴交点坐标为(0,8),
则S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知AB是Rt△ABC的斜边,中线AD=7,中线BE=4,则AB等于( )
A、2
| ||
B、5
| ||
C、5
| ||
| D、10 |
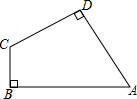 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=3,BC=2.求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=3,BC=2.求AB的长.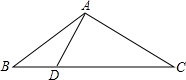 如图△ABC中,AB=AC=20,BC=32,D是BC上一点,且AD⊥AC,求BD的长.
如图△ABC中,AB=AC=20,BC=32,D是BC上一点,且AD⊥AC,求BD的长.