题目内容
16.如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准碟形,线段AB称为碟宽,顶点M称为蝶顶,点M到线段AB的距离称为碟高.(1)抛物线y=2x2对应的碟宽为1;抛物线y=ax2对应的碟宽为$\frac{2}{a}$;抛物线y=a(x-2)2+4(a>0)对应的碟宽为$\frac{2}{a}$.
(2)抛物线y=ax2-4ax-$\frac{5}{3}$(a>0)对应的碟宽为6,且在x轴上,求a的值.
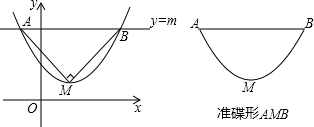
分析 (1)根据定义易算出含具体值的抛物线y=2x2的碟宽,利用端点(第一象限)横纵坐标的相等.推广至含字母的抛物线y=ax2(a>0),类似.而抛物线y=a(x-2)2+4(a>0)为顶点式,可看成y=ax2平移得到,则发现碟宽只和a有关.
(2)根据(1)的结论,根据碟宽易得关于a的方程$\frac{2}{a}$=6,解方程即可求得a的值.
解答 解:(1)∵a>0,
∴y=ax2的图象大致如下: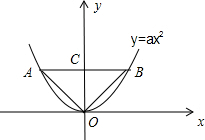
其必过原点O,记AB为其碟宽,AB与y轴的交点为C,连接OA,OB.
∵△OAB为等腰直角三角形,AB∥x轴,
∴OC⊥AB,
∴∠AOC=∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×90°=45°,
∴△ACO与△BCO亦为等腰直角三角形,
∴AC=OC=BC,
∴xA=yA,xB=yB,代入y=ax2,
∴A(-$\frac{1}{a}$,$\frac{1}{a}$),B($\frac{1}{a}$,$\frac{1}{a}$),C(0,$\frac{1}{a}$),
∴AB=$\frac{2}{a}$,OC=$\frac{1}{a}$,
即y=ax2的碟宽为$\frac{2}{a}$.
①抛物线y=2x2对应的a=2,得碟宽$\frac{2}{a}$为1;
②抛物线y=ax2(a>0),碟宽为$\frac{2}{a}$;
③抛物线y=a(x-2)2+4(a>0)可看成y=ax2向右平移2个单位长度,再向上平移4个单位长度后得到的图形,
∵平移不改变形状、大小、方向,
∴抛物线y=a(x-2)2+4(a>0)的准碟形≌抛物线y=ax2的准碟,
∵抛物线y=ax2(a>0),碟宽为$\frac{2}{a}$,
∴抛物线y=a(x-2)2+4(a>0),碟宽为$\frac{2}{a}$.
(2)∵y=ax2-4ax-$\frac{5}{3}$=a(x-2)2-(4a+$\frac{5}{3}$),
∴同(1),其碟宽为$\frac{2}{a}$,
∵y=ax2-4ax-$\frac{5}{3}$的碟宽为6,
∴$\frac{2}{a}$=6,
解得a=$\frac{1}{3}$.
故答案为:1;$\frac{2}{a}$;$\frac{2}{a}$.
点评 本题考查二次函数综合题,题目中主要涉及特殊直角三角形,二次函数解析式与图象性质,解题的关键是由抛物线y=ax2(a>0),得到碟宽只和a有关,即碟宽为$\frac{2}{a}$.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案( )
| A. | 18cm | B. | 19cm | C. | 24cm | D. | 19.5cm |
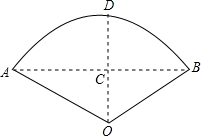 如图,有一管道要横跨一条河流,为了确保船只的通行,要把直管制成弧形,且要求管道距水面的最大高度为6m(即拱形高CD=6m),AB=12$\sqrt{3}$m,至少需要多少米长的直管?
如图,有一管道要横跨一条河流,为了确保船只的通行,要把直管制成弧形,且要求管道距水面的最大高度为6m(即拱形高CD=6m),AB=12$\sqrt{3}$m,至少需要多少米长的直管?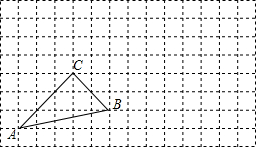 如图,把△ABC向右平移7个方格得到△A′B′C′,再绕点A′按逆时针方向旋转90度得到△A′B″C″.画出△A′B′C′和△A′B″C″,并标明对应字母.
如图,把△ABC向右平移7个方格得到△A′B′C′,再绕点A′按逆时针方向旋转90度得到△A′B″C″.画出△A′B′C′和△A′B″C″,并标明对应字母. 如图,把一个长方形的纸ABCD沿对角线折叠(长方形对边平行且相等,四个角是直角),重合部分三角形FBD是什么图形?请证明你的结论.
如图,把一个长方形的纸ABCD沿对角线折叠(长方形对边平行且相等,四个角是直角),重合部分三角形FBD是什么图形?请证明你的结论.