题目内容
5.若有理数x,y,z满足等式(x-1)2+(2x-y)4+|x-3z|=0,则(x+y)z2的值为$\frac{1}{3}$.分析 由非负数的性质可知x=1,y=2,z=$\frac{1}{3}$,然后代入计算即可.
解答 解:∵(x-1)2+(2x-y)4+|x-3z|=0,
∴x-1=0,2x-y=0,x-3z=0.
解得:x=1,y=2,z=$\frac{1}{3}$.
∴原式=3×($\frac{1}{3}$)2=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题主要考查的是求代数式的值,利用非负数的性质求得x=1,y=2,z=$\frac{1}{3}$是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.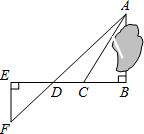 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )
为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )
 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )
为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )| A. | BC,∠ACB | B. | DE,DC,BC | C. | EF,DE,BD | D. | CD,∠ACB,∠ADB |
17. 如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
 如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |