题目内容
6. 如图,把一个长方形的纸ABCD沿对角线折叠(长方形对边平行且相等,四个角是直角),重合部分三角形FBD是什么图形?请证明你的结论.
如图,把一个长方形的纸ABCD沿对角线折叠(长方形对边平行且相等,四个角是直角),重合部分三角形FBD是什么图形?请证明你的结论.
分析 由轴对称的性质可以得出∠FBD=∠CBD,根据矩形的性质可以得出∠ADB=∠CBD,就可以得出∠FBD=∠FDB,而得出BF=DF证得△FBD是等腰三角形得出结论.
解答 答:重合部分△FBD是等腰三角形.
证明:∵折叠,
∴△EBD≌△CBD,
∴∠EBD=∠CBD.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∴∠FBD=∠FDB,
∴BF=DF,
∴重合部分△FBD是等腰三角形.
点评 考查了翻折变换的运用,矩形的性质的运用,等腰三角形的判定方法的运用,掌握折叠的性质是解决问题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
17. 如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
 如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
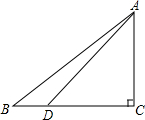 如图,在Rt△ABC中,∠C=90°,sin=$\frac{3}{5}$,点D在BC边上,DC=AC=6.
如图,在Rt△ABC中,∠C=90°,sin=$\frac{3}{5}$,点D在BC边上,DC=AC=6. 已知D、E两点在△ABC内,求作一点P,使PE=PD,且点P到∠B两边的距离相等(尺规作图,保留作图痕迹).
已知D、E两点在△ABC内,求作一点P,使PE=PD,且点P到∠B两边的距离相等(尺规作图,保留作图痕迹).