题目内容
1.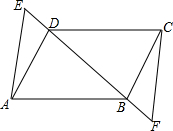 如图,在四边形ABCD中,点E、F在直线BD上,AE=CF,AD=CB,BE=DF.
如图,在四边形ABCD中,点E、F在直线BD上,AE=CF,AD=CB,BE=DF.(1)试判断△ADE与△CBF是否全等?并说明理由.
(2)试判断AD与BC是否平行,并说明理由.
分析 (1)由点E、F在直线BD上,得出BE=DF,由SSS证得:△ADE≌△CBF;
(2)由(1)证得∠ADE=∠CBF,再由∠ADE+∠ADB=∠CBF+∠CBD=180°,得出∠ADB=∠CBD,从而得出结论.
解答 解:(1)△ADE与△CBF全等;理由如下:
∵点E、F在直线BD上,BE=DF,
∴DE=BF,
在△ADE和△CBF中,$\left\{\begin{array}{l}{AE=CF}\\{AD=CB}\\{DE=BF}\end{array}\right.$,
∴△ADE≌△CBF(SSS);
(2)AD与BC平行;理由如下:
由(1)得:△ADE≌△CBF,
∴∠ADE=∠CBF,
∵∠ADE+∠ADB=∠CBF+∠CBD=180°,
∴∠ADB=∠CBD,
∴AD∥BC.
点评 本题考查了全等三角形的判定与性质、平行线的判定方法;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
18.数轴上到原点O距离2个单位长度的点表示的数是( )
| A. | -2 | B. | 2 | C. | -2或2 | D. | -2和0 |
 已知:如图,E是四边形ABCD的对角线BD上一点,且AB•AD=AC•AE,∠1=∠2.
已知:如图,E是四边形ABCD的对角线BD上一点,且AB•AD=AC•AE,∠1=∠2. 如图所示,已知△ABC.
如图所示,已知△ABC.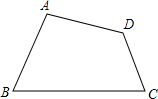 如图:四边形ABCD中,∠D=120°,∠C=75°,AD=4,CD=2$\sqrt{3}$-2,cosB=$\frac{3}{5}$,求BC的长.
如图:四边形ABCD中,∠D=120°,∠C=75°,AD=4,CD=2$\sqrt{3}$-2,cosB=$\frac{3}{5}$,求BC的长. 如图,AB=DC,BE=CF,AF=DE.求证:∠C=∠B.
如图,AB=DC,BE=CF,AF=DE.求证:∠C=∠B.