题目内容
18．已知一个三角形的两边长分别为2cm和4cm，第三边的长为偶数，则第三边的长为（ ）| A． | 2cm | B． | 3cm | C． | 4cm | D． | 6cm |
分析 利用三角形三边关系定理，先确定第三边的范围，进而就可以求出第三边的长．
解答 解：设第三边为acm，根据三角形的三边关系知，4-2＜a＜4+2．
即2＜a＜6，
由周长为偶数，
则a为4cm．
故选C．
点评 此题主要考查了三角形三边关系，要注意三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知：如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′
6．若三角形的两边长分别为6cm，9cm，则其第三边的长可能为（ ）
| A． | 2cm | B． | 3cm | C． | 7cm | D． | 16cm |
3．已知∠Α=25°，则它的余角是（ ）
| A． | 75° | B． | 65° | C． | 165° | D． | 155° |
10．下列调查中，适合普查的是（ ）
| A． | 一批手机电池的使用寿命 | B． | 中国公民保护环境的意识 | ||
| C． | 你所在学校的男、女同学的人数 | D． | 端午节期间苏州市场上粽子的质量 |
7．计算${（5\sqrt{5}）^2}$的结果是（ ）
| A． | 25 | B． | 125 | C． | $\sqrt{5}$ | D． | $25\sqrt{5}$ |
2．甲、乙两人在100米直道AB上练习匀速往返跑，若甲、乙分别从A，B两端同时出发，分别到另一端点处掉头，掉头时间不计．甲、乙两人距A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200）如图所示．综合图象信息解答下列问题：
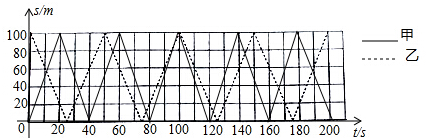
（1）求甲乙两人的速度；
（2）完成下列表格：
（3）在（2）的基础上，通过计算判断，当t=390s时，他们是否相遇？若相遇，应是第几次？并求出此时甲离A端的距离．
（1）求甲乙两人的速度；
（2）完成下列表格：
| 两人相遇次数（单位：次） | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和（单位：m） | 100 | 300 | 500 | 700 | … | 200n-100 |