题目内容
4.商场销售A、B两种商品,它们的进价和售价如表所示.| A商品 | B商品 | |
| 进价(元/件) | 30 | 40 |
| 售价(元/件) | 50 | 70 |
(2)该商场第二次购买A、B两种商品,而B商品数量比A商品数量的2倍少6件,且购买总额不超过2840元,总利润不少于1900元.请你帮助该商场设计相应的进货方案;
(3)若一个星期该商场销售A、B两种商品的总利润恰好是140元,求销售A、B两种商品各多少件?
分析 (1)首先设出未知数,根据题意可得两个等量关系:①A、B两种商品共60件,②进价用去2050元,可以列出方程组,解方程组即可;
(2)设该商场购进A种商品a件,则购进B种商品(2a-6)件,根据题意得:A商品的利润×数量+B商品的利润×数量≥1900,A商品的单价×数量+B商品的单价×数量≤2840,解不等式组即可;
(3)设该商场销售A种商品b件,销售B种商品c件,根据题意可得:20b+30c=140,进而求出b、c的值即可.
解答 解:(1)设该商场购进A种商品x件,B种商品y件,依题意得:
$\left\{\begin{array}{l}{x+y=60}\\{30x+40y=2050}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=35}\\{y=25}\end{array}\right.$.
答:该商场购进A种商品35件,B种商品25件.
(2)设该商场购进A种商品a件,则购进B种商品(2a-6)件,根据题意得:
$\left\{\begin{array}{l}{30a+40(2a-6)≤2860}\\{20a+30(2a-6)≥1900}\end{array}\right.$,
解得26≤a≤$\frac{310}{11}$,
∵a是正整数,
∴a=26,27,28,
所以进货方案有三种:
方案一:购进A种商品26件,购进B种商品46件
方案二:购进A种商品27件,购进B种商品48件
方案三:购进A种商品28件,购进B种商品50件;
(3)设该商场销售A种商品b件,销售B种商品c件,根据题意可得:20b+30c=140,
整理,得
2b+3c=14
b只能取1,4,
销售A种商品1件,B种商品4件或销售A种商品4件,B种商品2件.
点评 此题主要考查了一元一次不等式的应用以及选择最佳方案问题等知识,此题是中考中考查重点内容应重点掌握.

| 进价(元/台) | 售价(元/台) | |
| 电饭煲 | 200 | 250 |
| 电压锅 | 160 | 200 |
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的$\frac{5}{6}$,问橱具店有哪几种进货方案?全部售完时,哪种进货方案盈利最多?
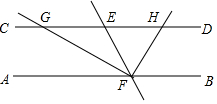 如图,直线EF分别与直线AB,CD相交于点F,E,FG平分∠AFE交CD于点G,FH平分∠BFE交CD于点H,若∠GEF=7∠FGE,AB∥CD,那么∠HFB=70°.
如图,直线EF分别与直线AB,CD相交于点F,E,FG平分∠AFE交CD于点G,FH平分∠BFE交CD于点H,若∠GEF=7∠FGE,AB∥CD,那么∠HFB=70°. 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为10$\sqrt{5}$.
如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为10$\sqrt{5}$. 将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,使点A1,A2,A3在直线y=x+1上,点C1,C2,C3在x轴上,若按此规律放置正方形A2017B2017C2017C2016,则点B2017的纵坐标为22016.
将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,使点A1,A2,A3在直线y=x+1上,点C1,C2,C3在x轴上,若按此规律放置正方形A2017B2017C2017C2016,则点B2017的纵坐标为22016.