题目内容
已知抛物线y=
(x-1)2-1.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为p,与x轴的交点为Q,求直线PQ的函数解析式?
| 1 |
| 4 |
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为p,与x轴的交点为Q,求直线PQ的函数解析式?
考点:二次函数的性质,待定系数法求一次函数解析式
专题:
分析:(1)根据二次函数的顶点式可直接得出抛物线的开口方向、对称轴;
(2)结合开口方向和顶点坐标可求得其最小值;
(3)可分别求得P、Q点的坐标,再利用待定系数法可求得直线PQ的解析式.
(2)结合开口方向和顶点坐标可求得其最小值;
(3)可分别求得P、Q点的坐标,再利用待定系数法可求得直线PQ的解析式.
解答:解:
(1)∵y=
(x-1)2-1,
∴开口向上,顶点坐标(1,-1);
(2)由(1)可知开口向上,所以函数y有最小值,最小值为-1;
(3)在y=
(x-1)2-1中,分别令x=0、y=0,可分别求得y=-1和x=3或-1,
∴P为(0,-1),Q点为(3,0)或(-1,0),
设直线PQ解析式为y=kx+b,
当P为(0,-1),Q为(3,0)时,代入可得
,可解得
,此时直线PQ解析式为y=
x-1;
当P为(0,-1),Q为(-,0)时,代入可得
,可解得
,此时直线PQ解析式为y=-x-1;
综上可知直线PQ的解析式为y=
x-1或y=-x-1.
(1)∵y=
| 1 |
| 4 |
∴开口向上,顶点坐标(1,-1);
(2)由(1)可知开口向上,所以函数y有最小值,最小值为-1;
(3)在y=
| 1 |
| 4 |
∴P为(0,-1),Q点为(3,0)或(-1,0),
设直线PQ解析式为y=kx+b,
当P为(0,-1),Q为(3,0)时,代入可得
|
|
| 1 |
| 3 |
当P为(0,-1),Q为(-,0)时,代入可得
|
|
综上可知直线PQ的解析式为y=
| 1 |
| 3 |
点评:本题主要考查二次函数的性质及待定系数法的应用,掌握二次函数的顶点式y=a(x-h)2+k的顶点坐标为(h,k)是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
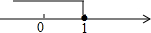 下列说法错误的是( )
下列说法错误的是( )| A、不等式x-3<-2的解集为x<1 |
| B、不等式x+2≤-2的最大负整数解为-1 |
| C、若不等式-3x+7<-2x成立,则不等式2x>9成立 |
| D、不等式-x≥-1的解集表示在数轴上如图所示 |
 已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE,求∠APD的度数.
已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE,求∠APD的度数. 如图,几块大小不等的正方形纸片无重叠地铺满了一块长方形.已知正方形纸片A的边长为7,求最小的正方形纸片的边长.
如图,几块大小不等的正方形纸片无重叠地铺满了一块长方形.已知正方形纸片A的边长为7,求最小的正方形纸片的边长. 如图,∠α可以表示成
如图,∠α可以表示成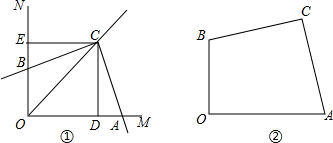
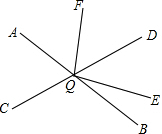 如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.
如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.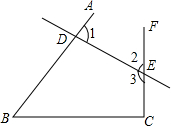 如图,
如图,