题目内容
 某几何体的三视图如图所示,其中主视图中半圆的半径为1.
某几何体的三视图如图所示,其中主视图中半圆的半径为1.(1)请用文字(或图形)描述该几何体的形状;
(2)求该几何体的表面积与体积.
考点:由三视图判断几何体
专题:
分析:(1)由三视图可知:该几何体是一个长、宽、高分别为4、3、2的长方体在上底面中间挖去一个直径为2的半圆柱;
(2)据(1)可计算出其表面积与体积.
(2)据(1)可计算出其表面积与体积.
解答:解:(1)由三视图可知:该几何体是一个长、宽、高分别为4、3、2的长方体在上底面中间挖去一个直径为2的半圆柱.

S表面积=3×2×2+3×4+3×1×2+(2×4-
π×12)×2+π×1×3=12+12+6+16-π+3π=46+2π.
V=4×3×2-
π×12×3=24-
π.

S表面积=3×2×2+3×4+3×1×2+(2×4-
| 1 |
| 2 |
V=4×3×2-
| 1 |
| 2 |
| 3 |
| 2 |
点评:此题考查有三视图判定几何体,由三视图正确恢复原几何体是解题的关键.

练习册系列答案
相关题目
一个点从数轴上的-3表示的点开始,先向右移动2个单位长度,再向左移动4个单位长度,这时该点所对应的数是( )
| A、3 | B、-5 | C、-1 | D、-9 |
计算:
+
=( )
| 1 |
| a |
| 1 |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
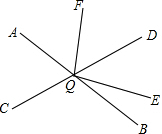 如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.
如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.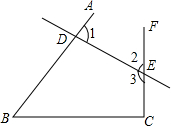 如图,
如图,