题目内容
10.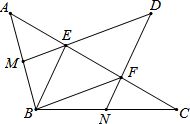 如图,在△ABC中,M,N分别是边AB、BC的中点,E、F是边AC上的三等分点,连接ME、NF且延长后交于点D,连接BE、BF
如图,在△ABC中,M,N分别是边AB、BC的中点,E、F是边AC上的三等分点,连接ME、NF且延长后交于点D,连接BE、BF(1)求证:四边形BFDE是平行四边形;
(2)若AB=3$\sqrt{2}$,∠A=45°,∠C=30°,求:四边形BFDE的面积.
分析 (1)由E、F是边AC上的三等分点,CF=EF=AE,可得N是BC中点,即可得FN是△CEB的中位线,根据三角形中位线的性质,可得FN∥BE,同理可证:ED∥BF,即可判定四边形BFDE是平行四边形;
(2)首先过点B作BH⊥AC于点H,由AB=3$\sqrt{2}$,∠A=45°,可求得BH与AH的长,又由∠C=30°,即可求得CH的长,则可求得△ABC的面积,又由E、F是边AC上的三等分点,即可求得答案.
解答 (1)证明:∵E、F是AC边上的三等分点,
∴CF=EF=AE,
∵N是BC中点,
∴FN是△CEB的中位线,
∴FN∥BE,即DF∥BE,
同理可证:ED∥BF,
∴四边形BFDE是平行四边形;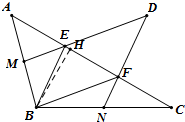 (2)解:过点B作BH⊥AC于点H,
(2)解:过点B作BH⊥AC于点H,
∵∠A=45°,AB=$3\sqrt{2}$,
∴BH=AH=3,
∵∠C=30°,
∴CH=$3\sqrt{3}$
∴${S_{△ABC}}=\frac{9}{2}({1+\sqrt{3}})$,
∵E、F是AC边上的三等分点,
∴${S_{△EBF}}=\frac{1}{3}{S_{△ABC}}=\frac{3}{2}({1+\sqrt{3}})$,
∴${S_{四边形BFDE}}=2{S_{△EBF}}=3({1+\sqrt{3}})=3+3\sqrt{3}$.
点评 此题考查了平行四边形的判定与性质、含30°角的直角三角形的性质以及等腰直角三角形性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
18.将800000用科学记数法表示为( )
| A. | 0.8×107 | B. | 8×105 | C. | 0.8×106 | D. | 80×104 |
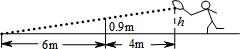 在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h=1.5m.
在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h=1.5m. 如图所示,已知函数y=x+b和y=ax-1的图象交点为M,则不等式x+b<ax-1的解集为x<-1.
如图所示,已知函数y=x+b和y=ax-1的图象交点为M,则不等式x+b<ax-1的解集为x<-1.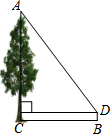 如图,B为地面上一点,测得点B到树底部C的距离为10米,在点B处放置一个1米高的测角仪BD,并测得树顶A的仰角为53°,则树高AC约为14.3 米(精确到0.1米).
如图,B为地面上一点,测得点B到树底部C的距离为10米,在点B处放置一个1米高的测角仪BD,并测得树顶A的仰角为53°,则树高AC约为14.3 米(精确到0.1米).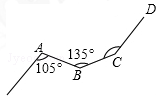 如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=150°.
如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=150°.