题目内容
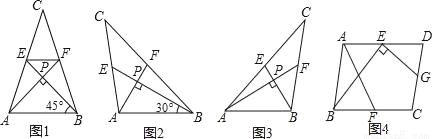
我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC﹣b,AB=c.
【特例探索】
(1)如图1,当∠ABE=45°,c=2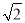 时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
【拓展应用】
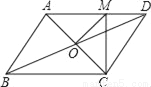
(3)如图4,在?ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2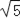 ,AB=3.求AF的长.
,AB=3.求AF的长.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
实验中学为了了解该校学生课外阅读情况,随机抽查了50名学生,统计他们平均每周课外阅读时间t(h).枨据时间t的长短分为A,B,C,D四类.下面是根据所抽杳的人数绘制了不完整的统计表.其中a、b、c和d是满足a<b<c<d的正整数,请解答下面的问题:
50名学生平均每天课外阅读时间统计表
类别 | A | B | C | D |
时间t(h) | t<1 | 1≤t<2 | 2≤t<3 | t≥3 |
人数 | 5a | 5b | 5c | 5d |
(1)写出表格中a+b+c+d的值.并求表格中的a、b、c、d的值;
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
(1)a+b+c+d=10,a=1,b=2,c=3,d=4;(2)22本(也可以是21本) 【解析】试题分析:(1)根据统计表可得5a+5b+5c+5d=50,a+b+c+d=10,再根据a<b<c<d,所以a≥1,b≥2,c≥3,d≥4,所以a+b+c+d≥10,a=1,b=2,c=3,d=4; (2)计算出一年阅读的总字数÷100000,即可解答. 试题解析:(1)5a+5b...

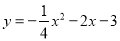 配方化为
配方化为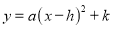 形式是( ).
形式是( ).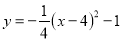 B.
B. 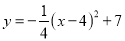
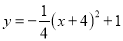 D.
D. 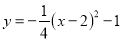
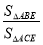 =
=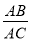 ;(3)
;(3)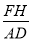 =
=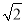 ﹣1;(4)四边形BEHF为菱形.正确的有几个( )
﹣1;(4)四边形BEHF为菱形.正确的有几个( )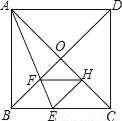
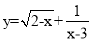 中自变量x的取值范围是( )
中自变量x的取值范围是( )
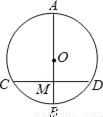
 ,一圆弧过点B和点C,且与AD相切,则图中阴影部分面积为______.
,一圆弧过点B和点C,且与AD相切,则图中阴影部分面积为______.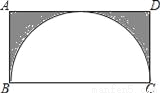
 C. 6 D. 6
C. 6 D. 6