题目内容
 如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为
如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为考点:轴对称-最短路线问题
专题:
分析:作BM⊥AC于M,交AD于F,根据三线合一定理求出BD的长和AD⊥BC,根据三角形面积公式求出BM,根据对称性质求出BF=CF,根据垂线段最短得出CF+EF≥BM,即可得出答案.
解答: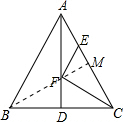 解:作BM⊥AC于M,交AD于F,
解:作BM⊥AC于M,交AD于F,
∵AB=AC=5,BC=6,AD是BC边上的中线,
∴BD=DC=3,AD⊥BC,AD平分∠BAC,
∴B、C关于AD对称,
∴BF=CF,
根据垂线段最短得出:CF+EF=BF+EF≥BF+FM=BM,
即CF+EF≥BM,
∵S△ABC=
×BC×AD=
×AC×BM,
∴BM=
=
=
,
即CF+EF的最小值是
,
故答案为:
.
 解:作BM⊥AC于M,交AD于F,
解:作BM⊥AC于M,交AD于F,∵AB=AC=5,BC=6,AD是BC边上的中线,
∴BD=DC=3,AD⊥BC,AD平分∠BAC,
∴B、C关于AD对称,
∴BF=CF,
根据垂线段最短得出:CF+EF=BF+EF≥BF+FM=BM,
即CF+EF≥BM,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BM=
| BC•AD |
| AC |
| 6×4 |
| 5 |
| 24 |
| 5 |
即CF+EF的最小值是
| 24 |
| 5 |
故答案为:
| 24 |
| 5 |
点评:本题考查了轴对称-最短路线问题,关键是画出符合条件的图形,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x=
+1,且x2=ax+b,则a,b的值分别为( )
| 5 |
| A、1,2 | B、2,2 |
| C、2,3 | D、2,4 |
 用半径R=8mm,r=5mm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=8.3mm(如图),计算出内孔直径D的大小(精确到0.1mm)
用半径R=8mm,r=5mm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=8.3mm(如图),计算出内孔直径D的大小(精确到0.1mm)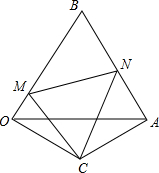 如图,△BOA是边长为2的等边三角形,OC=AC,∠OCA=120°,点M在OB边上,连接CM,将CM绕点C顺时针方向旋转60°,交AB于点N,连接MN,则△BMN的周长是
如图,△BOA是边长为2的等边三角形,OC=AC,∠OCA=120°,点M在OB边上,连接CM,将CM绕点C顺时针方向旋转60°,交AB于点N,连接MN,则△BMN的周长是 如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?
如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?
 如图,△ABC中点D、E分别在AB、AC上,且DE∥BC,已知BC=35,CE=15,DE=20,cosC=
如图,△ABC中点D、E分别在AB、AC上,且DE∥BC,已知BC=35,CE=15,DE=20,cosC=