题目内容

6．已知AB是⊙O的一条弦，在圆上找一点C，使得△ABC为等腰三角形．有满足条件的点C共有4个．

分析 根据垂径定理和等腰三角形的性质作出符合条件的点，即可得到答案．

解答 解：如图所示，
满足条件的点C共有4个．
故答案为：4．

点评 本题考查的是垂径定理和等腰三角形的性质，掌握垂直于弦的直径平分这条弦，并且平分弦所对的两条弧是解题的关键，注意分情况讨论思想的应用．

练习册系列答案
相关题目
16．如果盈利15万元记作+15万元，那么亏损3万元记作-3万元．
17．以下列各组线段为边，能组成三角形的是（　　）
A．4cm，6cm，8cmB．2cm，3cm，5cmC．5cm，6cm，12cmD．1cm，2cm，4cm
14．下列各式，计算正确的是（　　）
A．（-2）3=-23B．-14=（-1）4C．32=23D．（-1）3=-3
1．请用一元一次方程解决下面的问题：
（1）根据我省“十二五”铁路规划，徐州至连云港的客运专线项目建成后，两地间列车的最短客运时间将由现在的2小时18分钟缩短为36分钟，速每小时将提高260km，求提速后的车速度．（精确到1km/h）
（2）某小组计划做一批“中国结”，如果每人做6个，那么比计划多了8个；如果每人做4个，那么比计划少了42个．请你根据以上信息提出一个用一元一次方程解决的问题，并写出解答过程．
11．下列说法错误的是（　　）
A．平面上到角的两边的距离相等的点一定在角的平分线上
B．角平分线上任一点到角的两边的距离一定相等
C．一个角只有一条角平分线
D．一个角有无数条角平分线
18．把一元二次方程（x+2）（x-3）=4化成一般形式，得（　　）
A．x2+x-10=0B．x2-x-6=4C．x2-x-10=0D．x2-x-6=0
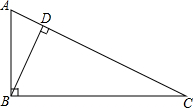15．解不等式组$\left\{\begin{array}{l}{4-x≥0，}&{①}\\{\frac{5x-1}{2}+1＞x，}&{②}\end{array}\right.$．
16．如图，在△ABC中，∠ABC=90°，△ABC∽△BDC，AB=3，AC=5，求DC的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网