题目内容
11.分别写出满足下列条件的一元二次方程:(1)有一个根为0;
(2)有一个根为-1;
(3)两根相等;
(4)两根互为相反数;
(5)两根互为倒数;
(6)两根分别为$1+\sqrt{3}$和$1-\sqrt{3}$.
分析 由根的定义:若方程有两根分别为x1,x2,则可得其中符合条件的方程为:(x-x1)(x-x2)=0;
(1)有一个根为0,另一个根没要求,代入上式可求得方程;
(2)有一个根为-1,另一个根没要求,代入上式可求得方程;
(3)只要两根相等,代入上式可求得方程;
(4)只要两根互为相反数,代入上式可求得方程;
(5)只要两根互为倒数,代入上式可求得方程;
(6)由两根分别为$1+\sqrt{3}$和$1-\sqrt{3}$,代入上式可求得方程.
解答 解:(1)如:x(x-1)=0,即x2-x=0;
(2)如:x(x+1)=0,即x2+x=0;
(3)如:(x+1)2=0,即x2+2x+1=0;
(4)如:x2-4=0;
(5)如:(x-3)(x-$\frac{1}{3}$)=0,即x2-$\frac{10}{3}$x+1=0;
(6)如:(x-1-$\sqrt{3}$)(x-1+$\sqrt{3}$)=0,即x2-2x-2=0.
点评 此题考查了方程根的意义.注意若方程有两根分别为x1,x2,则可得其中符合条件的方程为:(x-x1)(x-x2)=0.

练习册系列答案
相关题目
2.在Rt△ABC中,∠C=90°,∠A=60°,AC=6,则BC的长为( )
| A. | 6$\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 12 |
20.对于下列各数:-$\frac{4}{5}$,$\frac{2}{3}$,-6,0,-3.14,-0.25,其中负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
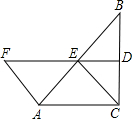 如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,F在DE的延长线上,且AF=CE=AE.
如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,F在DE的延长线上,且AF=CE=AE.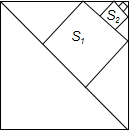 如图,在边长为a的大正方形中依次作小正方形S1,小正方形S2,…小正方形Sn,则小正方形Sn的边长为$\frac{\sqrt{2}}{{3}^{n}}$a.
如图,在边长为a的大正方形中依次作小正方形S1,小正方形S2,…小正方形Sn,则小正方形Sn的边长为$\frac{\sqrt{2}}{{3}^{n}}$a.