题目内容
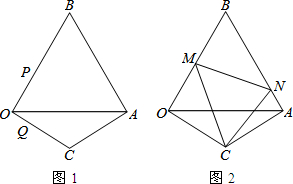
5.已知四边形四条边的长依次为2,4,7,x,求x的取值范围.分析 连接BD,根据三角形两边之和大于第三边,两边之差小于第三边,即可求得BD长的范围,进一步求得第四边长CD,即x的取值范围.
解答  解:设DA长为4,AB长为2,BC长为7,连接BD
解:设DA长为4,AB长为2,BC长为7,连接BD
BD长的范围4-2<BD<4+2,
即2<BD<6
同理可得|BD-BC|<CD<|BD+BC|,|6-7|<CD<|6+7|,即1<CD<13.
故x的取值范围为1<x<13.
点评 考查了三角形三边关系,关键是熟练掌握三角形三边关系定理:三角形两边之和大于第三边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.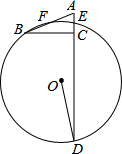 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 13 | B. | $2\sqrt{26}$ | C. | $3\sqrt{26}$ | D. | $\frac{27}{2}$ |
8.已知点(-2,y1),(-3,y2),(1,y3)在函数y=2x2+8x+7的图象上.则y1、y2、y3的大小关系是( )
| A. | y3<y2<y1 | B. | y2<y3<y1 | C. | y1<y2<y3 | D. | y1<y3<y2 |
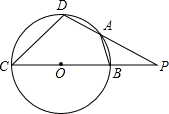 如图,BC为⊙O的直径,D,A是⊙O上两点,延长DA交CB延长线于点P,连接CD,AB.
如图,BC为⊙O的直径,D,A是⊙O上两点,延长DA交CB延长线于点P,连接CD,AB. 一个直棱柱的三视图如图所示(单位:mm),请描述这个直棱柱的形状,并画出它的表面展开图,求出它的表面积(结果保留3个有效数字).
一个直棱柱的三视图如图所示(单位:mm),请描述这个直棱柱的形状,并画出它的表面展开图,求出它的表面积(结果保留3个有效数字).