题目内容
9.从-3,-2-1,1,2,3六个数中任选一个数记为k,则使得关于x的分式方程$\frac{k+1}{x+1}$=k+2有解,且关于x的一次函数y=(k-1)x-2不经过第一象限的概率为$\frac{1}{3}$.分析 直接利用分式方程有解的意义以及一次函数图象的性质得出k可能的取值,进而得出答案.
解答 解:∵关于x的分式方程$\frac{k+1}{x+1}$=k+2有解,
∴整理得:x=$\frac{-1}{k+2}$,
则k+2≠1,解得:k≠-1,
∵关于x的一次函数y=(k-1)x-2不经过第一象限,
∴k-1<0,
解得:k<1,
故符合题意的只有:-2,-3,
则使得关于x的分式方程$\frac{k+1}{x+1}$=k+2有解,且关于x的一次函数y=(k-1)x-2不经过第一象限的概率为:$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题主要考查了概率公式以及分式方程有解的意义以及一次函数图象的性质,熟练应用分式方程有解的意义得出k的值是解题关键.

练习册系列答案
相关题目
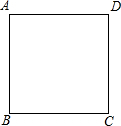 如图,正方形ABCD的面积和周长分别为S(cm)和C(cm),若长方形ABCD满足$\frac{S}{C}$=m,$\frac{AD}{AB}$=n,则称“m,n为长方形ABCD的特征数”.如,当AB=4,AD=12,$\frac{S}{C}$=$\frac{4×12}{2(4+12)}$=$\frac{3}{2}$,$\frac{AD}{AB}$=3,则长方形ABCD的特征数为“$\frac{3}{2}$,3”.
如图,正方形ABCD的面积和周长分别为S(cm)和C(cm),若长方形ABCD满足$\frac{S}{C}$=m,$\frac{AD}{AB}$=n,则称“m,n为长方形ABCD的特征数”.如,当AB=4,AD=12,$\frac{S}{C}$=$\frac{4×12}{2(4+12)}$=$\frac{3}{2}$,$\frac{AD}{AB}$=3,则长方形ABCD的特征数为“$\frac{3}{2}$,3”.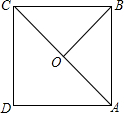 如图,在矩形ABCD中,O为对角线AC的中点,AB=3,AD=$\sqrt{7}$,则OB=( )
如图,在矩形ABCD中,O为对角线AC的中点,AB=3,AD=$\sqrt{7}$,则OB=( )