题目内容
13．
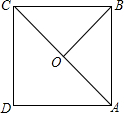如图，在矩形ABCD中，O为对角线AC的中点，AB=3，AD=$\sqrt{7}$，则OB=（ ）| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 由矩形的性质可知：CD=AB=3，由勾股定理可求得CA=4，由矩形的性质可知OB=$\frac{1}{2}AC$，从而可求得OB的长．
解答 解：∵ABCD为矩形，
∴CD=AB=3，∠D=90°．
在Rt△CAD中，由勾股定理得：AC=$\sqrt{C{D}^{2}+D{A}^{2}}$=$\sqrt{{3}^{2}+（\sqrt{7}）^{2}}$=4．
∵O是AC的中点，
∴OB=$\frac{1}{2}AC$=4×$\frac{1}{2}$=2．
故选：C．
点评 本题主要考查的是矩形的性质、勾股定理的应用，掌握矩形的性质是解题的关键．
练习册系列答案
相关题目
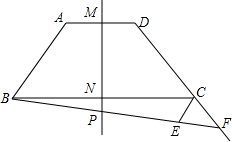已知等腰梯形ABCD中，AD∥BC，AD=4，BC=10，AB=CD=5，直线MN是等腰梯形的对称轴，P是射线MN上一点，射线BP交射线DC于点F，过C点作CE∥AB，与射线BP交于点E．
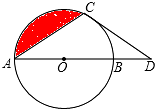如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，⊙O的半径为3，$\widehat{BC}$的长为π．
如图，在△ABC中，∠ABC、∠ACB的平分线BE、CD相交于点F，∠ABC=42°，∠A=60°，则∠BFC=120°．
2．在下列所给出坐标的点中，在第二象限的是（ ）
| A． | （1，-3） | B． | （-2，3） | C． | （3，4） | D． | （-1，-2） |