题目内容
13.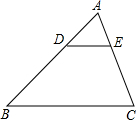 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}=\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的面积}{△ABC的面积}=\frac{1}{3}$ | D. | $\frac{△ADE的周长}{△ABC的周长}=\frac{1}{3}$ |
分析 由在△ABC中,DE∥BC,可得△ADE∽△ABC,然后由相似三角形的性质,求得答案.
解答 解:∵$\frac{AD}{DB}=\frac{1}{2}$,
∴$\frac{AD}{AB}$=$\frac{1}{3}$,
∵在△ABC中,DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{1}{3}$,
故A,B错误;
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{9}$,$\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$;
故C错误,D正确.
故选D.
点评 此题考查了相似三角形的判定与性质.注意证得△ADE∽△ABC,掌握对应关系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某公司销售部有营业员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量表:
(1)写出上表中数据的众数、中位数和平均数.
(2)若销售部把每位营业员的月销售额定为320件,你认为合理吗?如果不合理,你认为月销售额应定为多少?为什么?
| 每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(2)若销售部把每位营业员的月销售额定为320件,你认为合理吗?如果不合理,你认为月销售额应定为多少?为什么?
3.下列分式是最简分式的是( )
| A. | $\frac{2a}{5{a}^{2}}$ | B. | $\frac{a}{5{a}^{2}-2a}$ | C. | $\frac{a-2b}{a+b}$ | D. | $\frac{ab-{b}^{2}}{{a}^{2}-{b}^{2}}$ |
 如图:
如图: 如图,点A是双曲线y=$\frac{4}{x}$(x<0)上一点,AO的延长线交双曲线y=$\frac{{k}^{2}}{x}$(x>0,k>0)于点B,BC⊥x轴,若S△ABC=7.5,则k的值为3.
如图,点A是双曲线y=$\frac{4}{x}$(x<0)上一点,AO的延长线交双曲线y=$\frac{{k}^{2}}{x}$(x>0,k>0)于点B,BC⊥x轴,若S△ABC=7.5,则k的值为3.