题目内容
8.已知2x=m,3x=n,求6x+1的值.分析 根据幂的乘方和积的乘方,即可解答.
解答 解:6x+1=6x×6=(2×3)x×6=2x•3x•6=6mn.
点评 本题考查了幂的乘方和积的乘方,解决本题的关键是熟记幂的乘方和积的乘方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.运用完全平方公式计算79.82的最佳选择是( )
| A. | (79+0.8)2 | B. | (70+9.8)2 | C. | (80-0.2)2 | D. | (100-20.2)2 |
13.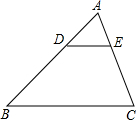 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}=\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的面积}{△ABC的面积}=\frac{1}{3}$ | D. | $\frac{△ADE的周长}{△ABC的周长}=\frac{1}{3}$ |
20.下面“去分母”后所得方程正确的是( )
| A. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2x=1 | |
| B. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2=x2-x | |
| C. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2x=x2-x | |
| D. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x(x-3)+2x=x-1 |
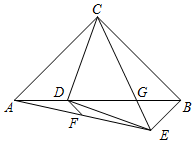 如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长2$\sqrt{2}$.
如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长2$\sqrt{2}$.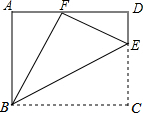 如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.