题目内容
5．二次函数y=x2-2x-3（2≤x≤5）的最小值是-3．分析 求开口向上的抛物线的最小值即求其定点的纵坐标，再由二次函数的顶点式解答即可．
解答 解：∵二次函数y=x2-2x-3可化为y=（x-1）2-4，
∴当x=1时，最小值是-4，
∵2≤x≤5，
∴当x=2时，y=x2-2x-3（2≤x≤5）的最小值是-3，
故答案为：-3．
点评 本题考查二次函数的最值，记住a＞O函数有最小值，a＜0函数有最大值，学会利用配方法确定函数最值问题，属于中考常考题型．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
15．如果一个数记成科学记数法后，10的指数是31，这个数的整数位数有（ ）
| A． | 29 | B． | 30 | C． | 31 | D． | 32 |
16．运用完全平方公式计算79.82的最佳选择是（ ）
| A． | （79+0.8）2 | B． | （70+9.8）2 | C． | （80-0.2）2 | D． | （100-20.2）2 |
13．
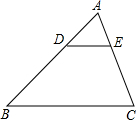如图，在△ABC中，DE∥BC，$\frac{AD}{DB}=\frac{1}{2}$，则下列结论中正确的是（ ）
如图，在△ABC中，DE∥BC，$\frac{AD}{DB}=\frac{1}{2}$，则下列结论中正确的是（ ）| A． | $\frac{AE}{AC}=\frac{1}{2}$ | B． | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C． | $\frac{△ADE的面积}{△ABC的面积}=\frac{1}{3}$ | D． | $\frac{△ADE的周长}{△ABC的周长}=\frac{1}{3}$ |
20．下面“去分母”后所得方程正确的是（ ）
| A． | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1，去分母，得x-3+2x=1 | |
| B． | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1，去分母，得x-3+2=x2-x | |
| C． | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1，去分母，得x-3+2x=x2-x | |
| D． | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1，去分母，得x（x-3）+2x=x-1 |
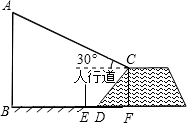如图，欲拆除一座垂直于地面的烟囱AB，距烟囱AB水平距离14米的D处有坡度为2：1，坝高（即CF）4米的背水坡大坝，在坝顶点C处测得烟囱顶端的仰角为30°，D，E之间是宽为2m的行人道，为确保行人安全，在拆除烟囱AB时，是否需要将此人行道封闭．（在地面上以点B为圆心，以AB长为半径的圆形区域为危险区域）（参考数值：$\sqrt{3}$≈1.7，$\sqrt{2}$≈1.4）
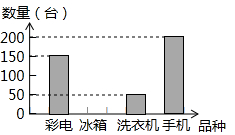为扩大内需，国务院决定在全国实施“家电下乡”政策．第一批列入家电下乡的产品为彩电、冰箱、洗衣机和手机四种产品．我市一家家电商场，去年一季度对以上四种产品的销售情况进行了统计．结果显示冰箱销售的数量占总销量的20%，手机销售的数量占总销量的40%，并绘制了如图的条形统计图，请你解答下列问题：
