题目内容
20.用两块斜边相等的三角板拼图.(1)当拼出图(1)的情形时,取BC的中点M,连接AM,DM,证明:△AMD为等腰三角形;
(2)拼成图(2),连接AD,点M,N分别是BC和AD的中点,证明:MN垂直平分AD.
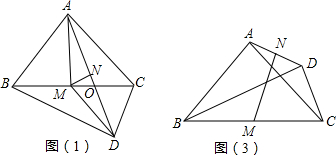
分析 (1)根据直角三角形斜边中线的性质即可解决问题.
(2)先证明MA=MD,再根据等腰三角形三线合一即可证明.
解答 证明:(1)如图1中,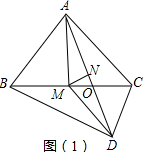
∵∠BAC=∠BDC=90°,BM=MC,
∴AM=$\frac{1}{2}$BC,DM=$\frac{1}{2}$BC,
∴MA=MD.
∴△MAD是等腰三角形.
(2)如图2中,连接AM、DM,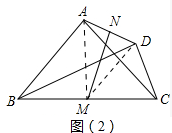
∵∠BAC=∠BDC=90°,BM=MC,
∴AM=$\frac{1}{2}$BC,DM=$\frac{1}{2}$BC,
∴MA=MD.
∵AN=ND,
∴MN⊥AD.
∴MN垂直平分AD.
点评 本题考查直角三角形斜边中线性质、等腰三角形的性质、线段垂直平分线的定义等知识,解题的关键是灵活运用直角三角形斜边中线等于斜边的一半,属于中考常考题型.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | a2+a3=a5 | B. | 4a+2b=6ab | C. | ${(\frac{1}{{{a^2}+1}})^0}=1$ | D. | ${(2\sqrt{5})^2}=10$ |
 双休日小明同学和爸爸约定从家出发到滨海森林湿地公园游玩,路途中经过安徽名人馆,因爸爸已经参观过安徽名人馆,所以小明提前从家骑自行车出发到达安徽名人馆参观一会后按照相同的速度前往滨湖森林湿地公园.小明同学出发45分钟后爸爸骑摩托车以小明2倍的速度直接前往滨湖森林湿地公园,爸爸出发半小时后在途中遇到小明,爸爸没有停留直接前往公园.结果爸爸比小明早7.5分钟到达滨湖森林湿地公园.如图是小明和爸爸各自行走路与骑车时间的函数图象.
双休日小明同学和爸爸约定从家出发到滨海森林湿地公园游玩,路途中经过安徽名人馆,因爸爸已经参观过安徽名人馆,所以小明提前从家骑自行车出发到达安徽名人馆参观一会后按照相同的速度前往滨湖森林湿地公园.小明同学出发45分钟后爸爸骑摩托车以小明2倍的速度直接前往滨湖森林湿地公园,爸爸出发半小时后在途中遇到小明,爸爸没有停留直接前往公园.结果爸爸比小明早7.5分钟到达滨湖森林湿地公园.如图是小明和爸爸各自行走路与骑车时间的函数图象.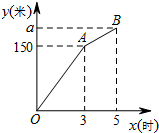 甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.
甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.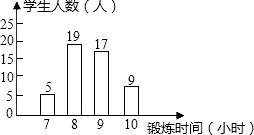 阳光体育运动,要求学生每一天锻炼一小时,如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图,那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时.
阳光体育运动,要求学生每一天锻炼一小时,如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图,那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时.