题目内容
6．圆内一弦与直径相交成30°，且分直径为2cm和10cm两部分，则该弦长为8$\sqrt{2}$cm．分析 根据题目中的条件，画出相应的图形，再根据垂径定理和勾股定理即可求得弦长，本题得以解决．
解答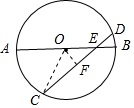 
解：如右图所示，AB为圆的直径，与弦CD相交的∠AEC=30°，AE=10cm，BE=2cm，
∴AB=12cm，
∴OE=4cm，
作OF⊥CD于点F，
∵OE=4cm，∠AEC=30°，
∴OF=2cm，
连接OC，
∴CF=$\sqrt{{6}^{2}-{2}^{2}}=4\sqrt{2}$，
∴CD=8$\sqrt{2}$cm，
故答案为：8$\sqrt{2}$．
点评 本题考查垂径定理、30°角所对的直角边与斜边的关系、勾股定理，解答本题的关键是明确题意，画出相应的图形，利用数形结合的思想解答．
练习册系列答案
相关题目
如图，在正方形ABCD中，AB=12，点E在边CD上，连接AE，将△ADE沿AE翻折，点D落在点F处，点O是对角线BD的中点，连接OF并延长与CD相交于点G，若$\frac{EF}{AB}$=$\frac{1}{3}$，则FG的长度是$\frac{4\sqrt{10}}{5}$．
如图，沿大等腰三角形的对称轴对折，则互相重合的两个小等腰三角形内的单项式的乘积为-4a2b4．
15．先阅读下面的材料，再解答后面的问题．
现代社会对保密要求越来越高，密码正在成为人们生活的一部分，有一种密码的明文（真实文）按计算器键盘字母排列分解，其中Q、W、E、…、N、M这26个字母依次对应1、2、3…、25、26这26个自然数（见表）：
给出一个变换公式：$\left\{\begin{array}{l}x'=\frac{x}{3}（x是自然数，1≤x≤26，x被3整除）\\ x'=\frac{x+2}{3}+17（x是自然数，1≤x≤26，x被3除余1）\\ x'=\frac{x+1}{3}+8（x是自然数，1≤x≤26，x被3除余2）\end{array}\right.$
如：将明文R转换成密文，R→4（4被3除余1）→$\frac{4+2}{3}$+17=19→L，即R变为L．
将明文A转换成密文，A→11（11被3除余2）→$\frac{11+1}{3}$+8=12→S，即A变为S．
再如：将密文X转换成明文，X→21→3×（21-17）-2=10→P，即X变为P；
将密文D转换成明文，D→13→3×（13-8）-1=14→F，即D变为F；
（1）按上述方法将明文NET译为密文；
（2）若按上述方法将明文译成的密文为DMN，请找出它的明文．
现代社会对保密要求越来越高，密码正在成为人们生活的一部分，有一种密码的明文（真实文）按计算器键盘字母排列分解，其中Q、W、E、…、N、M这26个字母依次对应1、2、3…、25、26这26个自然数（见表）：
| Q | W | E | R | T | Y | U | I | O | P | A | S | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| F | G | H | J | K | L | Z | X | C | V | B | N | M |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
如：将明文R转换成密文，R→4（4被3除余1）→$\frac{4+2}{3}$+17=19→L，即R变为L．
将明文A转换成密文，A→11（11被3除余2）→$\frac{11+1}{3}$+8=12→S，即A变为S．
再如：将密文X转换成明文，X→21→3×（21-17）-2=10→P，即X变为P；
将密文D转换成明文，D→13→3×（13-8）-1=14→F，即D变为F；
（1）按上述方法将明文NET译为密文；
（2）若按上述方法将明文译成的密文为DMN，请找出它的明文．
16．下列各组数不能组成三角形的是（ ）
| A． | $\sqrt{3}$，2，1 | B． | 5，7，12 | C． | 3，4，5 | D． | 0.7，2.4，2.5 |